题目内容
(本题满分12分)设函数f (x) =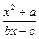 (b,c∈N*),若方程f(x) = x的解为0,2,且f (–2)<–
(b,c∈N*),若方程f(x) = x的解为0,2,且f (–2)<–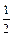 .(Ⅰ)试求函数f(x)的单调区间;(Ⅱ)已知各项不为零的数列{an}满足4Sn·f (
.(Ⅰ)试求函数f(x)的单调区间;(Ⅱ)已知各项不为零的数列{an}满足4Sn·f (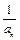 ) = 1,其中Sn为{an}的前n项和.求证:
) = 1,其中Sn为{an}的前n项和.求证: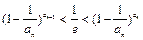 .
.
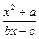 (b,c∈N*),若方程f(x) = x的解为0,2,且f (–2)<–
(b,c∈N*),若方程f(x) = x的解为0,2,且f (–2)<–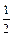 .(Ⅰ)试求函数f(x)的单调区间;(Ⅱ)已知各项不为零的数列{an}满足4Sn·f (
.(Ⅰ)试求函数f(x)的单调区间;(Ⅱ)已知各项不为零的数列{an}满足4Sn·f (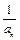 ) = 1,其中Sn为{an}的前n项和.求证:
) = 1,其中Sn为{an}的前n项和.求证: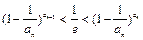 .
.(Ⅰ)f(x)的单调递增区间为(–∞,0),(2,+∞)单调递减区间为(0,1),(1,2)(Ⅱ) 略
(Ⅰ)解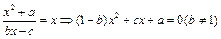

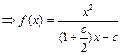 .------(2分)
.------(2分)
由f (–2) =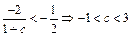 又∵b,c∈N* ∴c = 2,b = 2
又∵b,c∈N* ∴c = 2,b = 2
∴f (x) =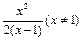 .-------(4分)
.-------(4分)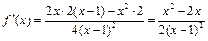
令f′(x)>0得:x<0或x>2,令f′(x)<0得:0<x<2∴f(x)的单调递增区间为(–∞,0),
(2,+∞)f(x)的单调递减区间为(0,1),(1,2)--------(6分)
(Ⅱ)证明:由已知可得:2Sn = an –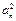 ,
,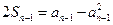
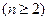
两式相减得:(an + an – 1) (an – an – 1+1) =" 0" (n≥2)∴an = –an–1或an –an–1 =" –1 " -(7分)
当n ="1" 时,2a1 = a1 –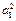
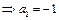
若an = –an–1,则a2 = –a1 = 1与an≠1矛盾.(定义域要求an≠1)∴an – an–1 = 1,∴an= –n.(8分)
要证的不等式转化为
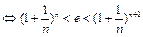
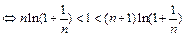
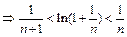
先证不等式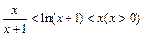 令g (x) = x –ln(1 + x),h(x) = ln(x +1) –
令g (x) = x –ln(1 + x),h(x) = ln(x +1) –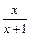 -----(10分)
-----(10分)
则g′(x) =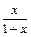 ,h′(x) =
,h′(x) =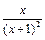 ∵x>0 ∴g′(x)>0,h′(x)>0∴g (x), h(x)在(0,+∞)上单调递增,
∵x>0 ∴g′(x)>0,h′(x)>0∴g (x), h(x)在(0,+∞)上单调递增,
∴g (x)>g (0) = 0,h(x)>h(0) =" 0 " ∴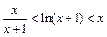 。
。
故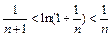 ,即
,即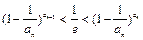 -----(12分)
-----(12分)
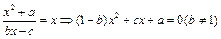

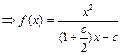 .------(2分)
.------(2分)由f (–2) =
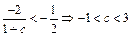 又∵b,c∈N* ∴c = 2,b = 2
又∵b,c∈N* ∴c = 2,b = 2∴f (x) =
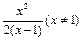 .-------(4分)
.-------(4分)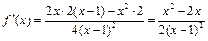
令f′(x)>0得:x<0或x>2,令f′(x)<0得:0<x<2∴f(x)的单调递增区间为(–∞,0),
(2,+∞)f(x)的单调递减区间为(0,1),(1,2)--------(6分)
(Ⅱ)证明:由已知可得:2Sn = an –
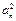 ,
,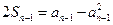
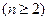
两式相减得:(an + an – 1) (an – an – 1+1) =" 0" (n≥2)∴an = –an–1或an –an–1 =" –1 " -(7分)
当n ="1" 时,2a1 = a1 –
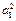
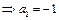
若an = –an–1,则a2 = –a1 = 1与an≠1矛盾.(定义域要求an≠1)∴an – an–1 = 1,∴an= –n.(8分)
要证的不等式转化为

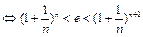
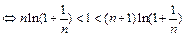
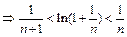
先证不等式
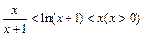 令g (x) = x –ln(1 + x),h(x) = ln(x +1) –
令g (x) = x –ln(1 + x),h(x) = ln(x +1) –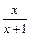 -----(10分)
-----(10分)则g′(x) =
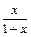 ,h′(x) =
,h′(x) =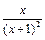 ∵x>0 ∴g′(x)>0,h′(x)>0∴g (x), h(x)在(0,+∞)上单调递增,
∵x>0 ∴g′(x)>0,h′(x)>0∴g (x), h(x)在(0,+∞)上单调递增,∴g (x)>g (0) = 0,h(x)>h(0) =" 0 " ∴
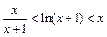 。
。故
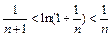 ,即
,即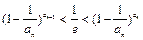 -----(12分)
-----(12分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图像关于原点对称,其中m,n为实常数。
的图像关于原点对称,其中m,n为实常数。 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。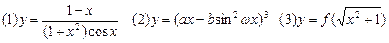
 cos2t+
cos2t+ 满足
满足
 0,则必有( ).
0,则必有( ).



 ,
, .
. 的单调区间;
的单调区间; 内是减函数,求
内是减函数,求 的取值范围.
的取值范围. ,求
,求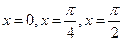 时
时 的值。
的值。