题目内容
函数f(x)=
在（-∞，n）∪（n+2，+∞）为奇函数，求m+n的值．
| x+m | x2-3 |
分析：利用奇函数定义域的对称性及奇函数的定义，即可求m，n的值，从而可得结论．
解答：解：∵函数f(x)=
在（-∞，n）∪（n+2，+∞）为奇函数，
∴n+n+2=0，f（-x）+f(x)=
+
=0
∴n=-1，m=0
∴m+n=-1
| x+m |
| x2-3 |
∴n+n+2=0，f（-x）+f(x)=
| -x+m |
| x2-3 |
| x+m |
| x2-3 |
∴n=-1，m=0
∴m+n=-1
点评：本题考查函数的奇偶性，正确运用奇函数的定义是解题的关键．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
其中P，M为实数集R的两个非空子集，又规定f(P)={y|y=f(x),x∈P}，f(M)={y|y=f(x),x∈M}.给出下列四个判断：
，则f(P)∩f(M)=
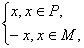其中P，M为实数集R的两个非空子集，又规定f(P)={y|y=f(x),x∈P}，f(M)={y|y=f(x),x∈M}.给出下列四个判断：①若P∩M=
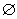，则f(P)∩f(M)=