题目内容
函数f(x)=![]() 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:
①若P∩M=![]() ,则f(P)∩f(M)=
,则f(P)∩f(M)=![]() ; ②若P∩M≠
; ②若P∩M≠![]() ,则f(P)∩f(M) ≠
,则f(P)∩f(M) ≠![]() ;
;
③若P∪M=R,则f(P)∪f(M)=R; ④若P∪M≠R,则f(P) ∪f(M)≠R.
其中正确判断有 ( )
A 0个 B 1个 C 2个 D 4个
A
解析:
①②③④错
若P={1}, M={- 1}则f(P)={1},f(M)={1} 则f(P)∩f(M) ≠![]() 故①错
故①错
若P={1,2}, M={1}则f(P)={1,2},f(M)={1}则f(P)∩f(M) =![]() 故②错
故②错
若P={非负实数},M={负实数}则f(P)={ 非负实数},f(M)={ 正实数} 则f(P) ∪f(M)≠R.
故③错
若P={非负实数},M={正实数}则f(P)={ 非负实数},f(M)={ 负实数} 则f(P) ∪f(M)=R.
故④错

练习册系列答案
相关题目
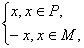 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=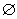 ,则f(P)∩f(M)=
,则f(P)∩f(M)=