题目内容
已知函数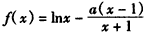
，
(Ⅰ)若函数f(x)在(0，+∞)上为单调增函数，求a的取值范围；
(Ⅱ)设m，n∈R+，且m≠n，求证：
。
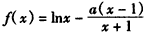，(Ⅰ)若函数f(x)在(0，+∞)上为单调增函数，求a的取值范围；
(Ⅱ)设m，n∈R+，且m≠n，求证：
。 (Ⅰ)解：
，
因为f（x）在(0，+∞)为单调增函数，
所以f′(x)≥0在（0，十∞）上恒成立，即x2+(2-2a)x+l≥0在(0，+∞)上恒成立，
当x∈(0，+∞)时，由x2+(2-2a)x+l≥0，
得
，
设
，
，
所以，当且仅当
，即x=1时，g（x）有最小值2，
所以2a-2≤2，所以，a≤2，
所以a的取值范围是(-∞，2]。
(Ⅱ)不妨设m＞n＞0，则
，
要证
，只需证
，
即证
，只需证
，
设
，
由(Ⅰ)知，h（x）在（1，+∞）上是单调增函数，
又
，
所以，
，即
成立，
所以，
。
，因为f（x）在(0，+∞)为单调增函数，
所以f′(x)≥0在（0，十∞）上恒成立，即x2+(2-2a)x+l≥0在(0，+∞)上恒成立，
当x∈(0，+∞)时，由x2+(2-2a)x+l≥0，
得
，设
，，所以，当且仅当
，即x=1时，g（x）有最小值2，所以2a-2≤2，所以，a≤2，
所以a的取值范围是(-∞，2]。
(Ⅱ)不妨设m＞n＞0，则
，要证
，只需证，即证
，只需证，设
，由(Ⅰ)知，h（x）在（1，+∞）上是单调增函数，
又
，所以，
，即成立，所以，
。
练习册系列答案
相关题目
已知函数y=y=
已知函数f（x）的定义域为[-3，+∞），部分函数值如表所示，其导函数的图象如图所示，若正数a，b满足f（2a+b）＜1，则
.
的值域为
，求
的值；
的值域.
，
在[l，+∞]上是增函数，求实数
的取值范围。
=一
是