题目内容

如图，已知椭圆的中心在坐标原点，焦点F1，F2在x轴上，长轴A1A2的长为4，左准线l与x轴的交点为M，|MA1|∶|A1F1|＝2∶1．

   (Ⅰ)求椭圆的方程；

  

(Ⅱ)若直线l1：x＝m(|m|＞1)，P为l1上的动点，使∠F1PF2最大的点P记为Q，求点Q的坐标(用m表示)．

：（Ｉ）设椭圆方程为（），半焦距为c, 则,,

由题意，得  ,    解得，故椭圆方程为

（II）设P(

当时，

当时, ，只需求的最大值即可.

直线的斜率，直线的斜率

当且仅当=时，最大，


解析:

：（1）待定系数法；（2）利用夹角公式将∠F1PF2的正切值用y0表示出来，利用基本不等式求其最值.

练习册系列答案
相关题目
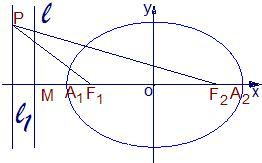精英家教网如图，已知椭圆的中心在坐标原点，焦点F1，F2在x轴上，长轴A1A2的长为4，左准线l与x轴的交点为M，|MA1|：|A1F1|=2：1．
（Ⅰ）求椭圆的方程；
（Ⅱ）若直线l1：x=m（|m|＞1），P为l1上的动点，使∠F1PF2最大的点P记为Q，求点Q的坐标（用m表示）．
精英家教网如图，已知椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的2倍且经过点M（2，1），平行于OM的直线l在y轴上的截距为m（m≠0），l交椭圆于A、B两个不同点．
（1）求椭圆的方程；
（2）求m的取值范围；
（3）求证直线MA、MB与x轴始终围成一个等腰三角形．
如图，已知椭圆的中心在原点，焦点在x轴上，离心率为
3
2
，且经过点M（4，1）．直线l：y=x+m交椭圆于A，B两不同的点．
（1）求椭圆的方程；
（2）当|AB|=
12
5
2
时，求m的值；
（3）若直线l不过点M，求证：直线MA，MB与x轴围成一个等腰三角形．
如图，已知椭圆的中心在坐标原点，焦点在x轴上，它的一个顶点为A（0，
2
），且离心率为
3
2
．
（ I）求椭圆的标准方程；
（ II）过点M（0，2）的直线l与椭圆相交于不同两点P、Q，点N在线段PQ上．设
|
MP
|
|
PN
|
=
|
MQ
|
|
NQ
|
=λ，试求实数λ的取值范围．
（2012•马鞍山二模）如图，已知椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的2倍且经过点M（2，1），平行于OM的直线l在y轴上的截距为m（m≠0），直线l交椭圆于A、B两个不同点（A、B与M不重合）．
（Ⅰ）求椭圆的方程；
（Ⅱ）当MA⊥MB时，求m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网