题目内容
已知函数 在
在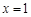 处取得极值.
处取得极值.
(1)求实数 的值;
的值;
(2)若关于 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)若
 ,使
,使 成立,求实数
成立,求实数 的取值范围
的取值范围
⑴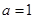 , (2)
, (2) 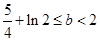 (3)
(3)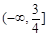
解析试题分析:⑴先求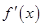 再解方程
再解方程 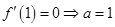 .(2)由
.(2)由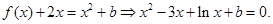 构造函数
构造函数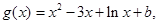 然后求
然后求 ,再解方程
,再解方程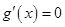 ,确定
,确定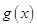 的单调区间,然后确定
的单调区间,然后确定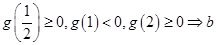 的取值范围. (3)由
的取值范围. (3)由
 ,使
,使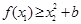 成立
成立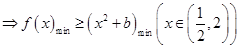 ,利用导数求
,利用导数求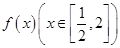 的最小值,利用二次函数求
的最小值,利用二次函数求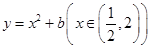 的最小值,解不等式求
的最小值,解不等式求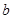 的范围.
的范围.
试题解析: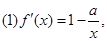 由题意得
由题意得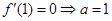 4分
4分
(2)由⑴得
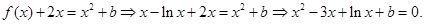
设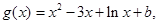 则
则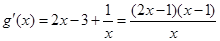 当
当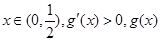 单调递增,
单调递增, 单调递减,
单调递减,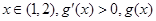 单调递增.
单调递增.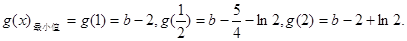 7分
7分
方程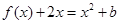 在
在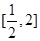 上恰有两个不等的实数根,则
上恰有两个不等的实数根,则 ,
,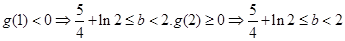 9分
9分
(3)依条件, 时
时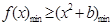
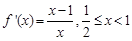 时
时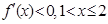 时
时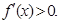
∴ 在
在 上为减函数,在
上为减函数,在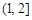 上为增函数
上为增函数
∴ 12分
12分
而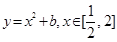 的最小值为
的最小值为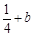
∴ ∴
∴ ∴
∴ 的取值范围为
的取值范围为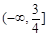 14分
14分
考点:求导数,应用导数求单调区间最值,构造函数法,解不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. .
. 在
在 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.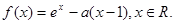
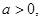 求函数
求函数 在
在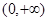 上的极值;
上的极值;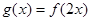 ,设函数
,设函数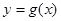 的图像
的图像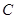 与
与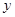 轴交于
轴交于 点,曲线
点,曲线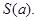 则当
则当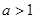 时,求
时,求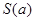 的最小值.
的最小值.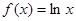
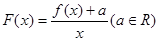 ,求
,求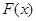 的极大值;
的极大值;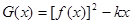 在定义域内单调递减,求满足此条件的实数k的取值范围.
在定义域内单调递减,求满足此条件的实数k的取值范围. (
( R),且该函数曲线
R),且该函数曲线 在
在 处的切线与
处的切线与 轴平行.
轴平行. 的单调性;
的单调性; 时,
时, .
.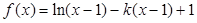 .
.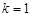 时,求函数
时,求函数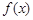 的最大值;
的最大值;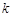 的取值范围;
的取值范围; (
( ).
).  时,求函数
时,求函数 的单调区间;
的单调区间; 时,
时,
 上的最小值;
上的最小值;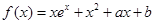 在点
在点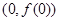 处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+
处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+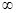 )均有
)均有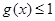 恒成立.
恒成立.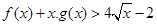 .
.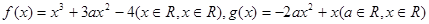 (Ⅰ)若函数
(Ⅰ)若函数 在
在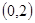 上单调递减,在区间
上单调递减,在区间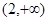 单调递增,求
单调递增,求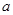 的值;
的值;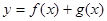 在
在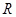 上有两个不同的极值点,求
上有两个不同的极值点,求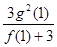 的取值范围;
的取值范围;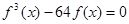 有且只有三个不同的实根,求
有且只有三个不同的实根,求