题目内容
已知抛物线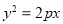 (
(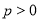 )的准线与
)的准线与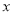 轴交于点
轴交于点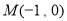 .
.
(1)求抛物线的方程,并写出焦点坐标;
(2)是否存在过焦点的直线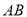 (直线与抛物线交于点
(直线与抛物线交于点 ,
,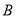 ),使得三角形
),使得三角形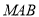 的面积
的面积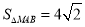 ?若存在,请求出直线
?若存在,请求出直线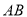 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(1) ,焦点坐标为
,焦点坐标为 ;
;
(2)存在,直线 的方程为:
的方程为: 或
或 ..
..
【解析】
试题分析:(1)根据抛物线的性质知抛物线的交点坐标为 ;
;
(2)设 与抛物线方程联立,由韦达定理,得到
与抛物线方程联立,由韦达定理,得到 ,进一步
,进一步 的面积用
的面积用 和表示,解得
和表示,解得 的值,得到所求直线方程.
的值,得到所求直线方程.
试题解析:(1)由已知得: ,从而抛物线方程为
,从而抛物线方程为 ,焦点坐标为
,焦点坐标为 .
.
(2)由题意,设
 ,并与
,并与 联立, 得到方程:
联立, 得到方程: ,
,
设 ,
, ,则
,则 ,
, .
.

∵ ,∴
,∴

 ,
,
又 ,∴
,∴ 解得
解得 ,
,
故直线 的方程为:
的方程为: .即
.即 或
或 .
.
解法二:(1)(同解法一)
(2)当 轴时,
轴时, ,
, ,
,
不符合题意.
故设
 (
( ),并与
),并与 联立,
联立,
得到方程: ,
,
设 ,
, ,则
,则 ,
, .
.

 ,
,
点 到直线
到直线 的距离为
的距离为 ,
,
∴

 ,
,
解得 ,
,
故直线 的方程为:
的方程为: .即
.即 或
或 .
.
考点:1.抛物线的标准方程;2.韦达定理.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 中,
中, 与平面
与平面 所成的角为
所成的角为 ,则
,则 所成的角为 .(结果用反三角函数表示)
所成的角为 .(结果用反三角函数表示)
 中,已知
中,已知 ,则该
,则该 ,始终平分圆
,始终平分圆 的周长,则
的周长,则 的最小值为 ( )
的最小值为 ( ) C.
C. D.5
D.5 中,已知
中,已知 ,则
,则 ( )
( ) B、
B、 C、
C、 D、
D、
 的焦点
的焦点 和点
和点 ,
, 为抛物线上一点,则
为抛物线上一点,则 的最小值是______________
的最小值是______________
 B.
B. C.36 D.
C.36 D.
 D.14+6
D.14+6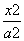 +
+ =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( )
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( )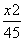 +
+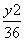 =1 B.
=1 B.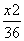 +
+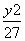 =1
=1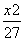 +
+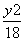 =1 D.
=1 D.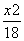 +
+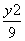 =1
=1