Question

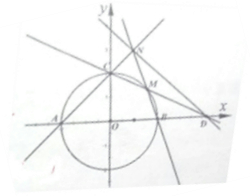如图，圆O：x²+y²=4与坐标轴交于点A，B，C．
（1）求与直线AC垂直的圆的切线方程；
（2）设点M是圆上任意一点（不在坐标轴上），直线CM交x轴于点D，直线BM交直线AC于点N，
    ①若D点坐标为（2

3

，0），求弦CM的长；
    ②求证：2k_ND-k_MB为定值．

Answer 1

考点：圆的切线方程,直线与圆锥曲线的关系

专题：计算题,直线与圆

分析：（1）先求直线AC的方程，设出切线方程，利用点线距离等于半径，即可求与直线AC垂直的圆的切线方程；
（2）①求出CM的方程，圆心到直线CM的距离，即可求弦CM的长；
②确定N，D的坐标，表示出2k_ND-k_MB，即可证明2k_ND-k_MB为定值．

解答： 解：（1）由题意，A（-2，0），B（2，0），C（0，2），
∴直线AC：

x

-2

+

y

2

=1，即x-y+2=0，…（2分）
设l：x+y+b=0，∴

|b|

1+1

=2，则b=±2

2

，
∴l：x+y±2

2

=0； …（5分）
（2）①CM：x+

3

y-2

3

=0，圆心到直线CM的距离d=

2 3

1+3

=

3

，
∴弦CM的长为2

4-3

=2   …（9分）
②设M（x₀，y₀），则x₀≠±2，x₀≠0，x₀²+y₀²=4，直线CM：y=

y0-2

x0

x+2，
则D（

2x0

2-y0

，0），k_MB=

y0

x0-2

，直线BM：y=

y0

x0-2

（x-2），
又l_AC：y=x+2AC与BM交点N（

4-2x0-2y0

x0-y0-2

，

-4y0

x0-y0-2

），k_ND=

4y0-2y02

x02-2x0y0+4y0-4-y02

将x₀²=4-y₀²，代入得k_ND=

y0-2

x0+y0-2

，…（13分）
所以2k_ND-k_MB=2×

y0-2

x0+y0-2

-

y0

x0-2

=1为定值．…（16分）

点评：本题考查直线方程，考查直线与圆的位置关系，考查学生的计算能力，属于中档题．