题目内容
过双曲线
-
=1(a>0,b>0)的右焦点F做一条斜率小于0的直线,且该直线与一条渐近线垂直,垂足为点A,与另一条渐近线交于点B,
=2
,则此双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| FB |
| FA |
考点:双曲线的简单性质
专题:计算题,平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析:由向量的共线定理可得A为FB的中点,OA为FB的垂直平分线,运用等腰三角形的知识,再由F到直线OA的距离即为b,求得OA=a,再由渐近线的对称性,即可得到∠AOF=60°,由离心率公式,结合解直角三角形即可得到所求值.
解答:
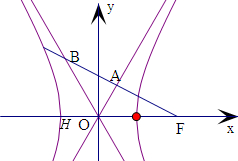 解:如图,
解:如图,
=2
,则A为FB的中点,
OA为FB的垂直平分线,
则|OB|=|OF|=c,
由渐近线y=
x,F(c,0),
|AF|=
=b,
即有|OA|=
=a,
由于∠AOF=∠AOB=∠BOH=60°,
则离心率e=
=
=2.
故答案为:2.
 解:如图,
解:如图,| FB |
| FA |
OA为FB的垂直平分线,
则|OB|=|OF|=c,
由渐近线y=
| b |
| a |
|AF|=
|
| ||||
|
即有|OA|=
| c2-b2 |
由于∠AOF=∠AOB=∠BOH=60°,
则离心率e=
| c |
| a |
| 1 |
| cos60° |
故答案为:2.
点评:本题考查双曲线的方程和性质,考查平面向量的共线定理,考查单调直线的距离公式,考查等腰三角形的性质和解直角三角形的知识,注意运用几何法,可简化运算过程,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
函数f(x)的导函数为f′(x),对?x∈R,都有2f′(x)>f(x)成立,若f(ln4)=2,则不等式f(x)>e
的解是( )
| x |
| 2 |
| A、x>ln4 |
| B、0<x<ln4 |
| C、x>1 |
| D、0<x<1 |
将一颗骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b,设任意投掷两次使两条不重合直线l1:ax+by=2,l2:x+2y=2平行的概率为P1,相交的概率为P2,若点(P1,P2)在圆(x-m)2+y2=
的内部,则实数m的取值范围是( )
| 137 |
| 144 |
A、(-
| ||||
B、(-∞,
| ||||
C、(-
| ||||
D、(-
|
 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=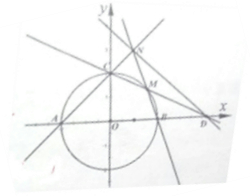 如图,圆O:x2+y2=4与坐标轴交于点A,B,C.
如图,圆O:x2+y2=4与坐标轴交于点A,B,C.