题目内容
(12分)已知椭圆C: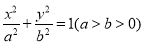 过点
过点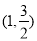 ,且椭圆C的离心率为
,且椭圆C的离心率为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若动点P在直线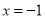 上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线
上,过P作直线交椭圆C于M,N两点,且P为线段MN中点,再过P作直线 .证明:直线
.证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
(Ⅰ)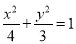 ;(Ⅱ)
;(Ⅱ)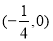
【解析】
试题分析:(Ⅰ)由椭圆过点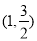 ,且椭圆C的离心率为
,且椭圆C的离心率为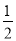 ,建立关于
,建立关于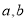 的方程组,可解得
的方程组,可解得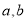 的值,即可得椭圆的方程.
的值,即可得椭圆的方程.
(Ⅱ)由点P的横坐标为-1,并且点P是MN的中点.直线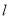 有两种情况,斜率存在时联立直线
有两种情况,斜率存在时联立直线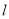 的方程与椭圆方程,消去y,由x的二次方程根据韦达定理,再写出直线
的方程与椭圆方程,消去y,由x的二次方程根据韦达定理,再写出直线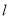 的方程,即可得到直线
的方程,即可得到直线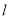 过定点.另外再检验斜率不存在的时同样过定点.由此即可的结论.
过定点.另外再检验斜率不存在的时同样过定点.由此即可的结论.
试题解析:(Ⅰ)因为点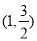 在椭圆C上,所以
在椭圆C上,所以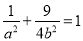 ,又椭圆C的离心率为
,又椭圆C的离心率为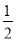 ,所以
,所以 ,
,
即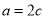 ,所以
,所以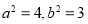 ,所以椭圆C的方程为
,所以椭圆C的方程为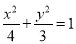
(Ⅱ)设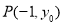 ,
,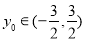 ,
,
①当直线MN的斜率存在时,设直线MN的方程为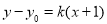 ,
,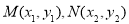 ,
,
由 ,得
,得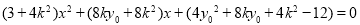 ,
,
所以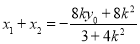 ,因为P为MN中点,所以
,因为P为MN中点,所以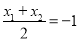 ,即
,即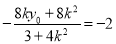 ,
,
所以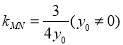 ,因为直线
,因为直线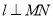 ,所以
,所以 ,所以直线的方程为
,所以直线的方程为
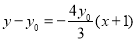 ,即
,即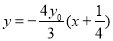 ,显然直线恒过定点
,显然直线恒过定点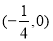
②当直线MN的斜率不存在时,直线MN的方程为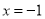 ,
,
此时直线为x轴,也过点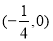 综上所述,直线恒过定点
综上所述,直线恒过定点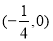
(此题还可以用点差法)
考点:1.椭圆的方程的性质.2.直线与椭圆的位置关系.3.分类思想.4.运算能力.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,
, ,棱
,棱 ,
, 分别是
分别是 、
、 的中点.
的中点.
 的长;
的长;  的值;
的值; .
. ,
, .若
.若 ,则实数
,则实数 的值是( )
的值是( ) B.
B.
 或
或 的导函数
的导函数 的图像如图所示,那么
的图像如图所示,那么 的图像最有可能的是( )
的图像最有可能的是( )
 ,
, .若
.若 ,则实数
,则实数 的值是( )
的值是( ) B.
B.
 或
或
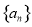 的前n项和为
的前n项和为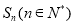 ,且满足
,且满足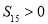 ,
,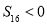 ,则
,则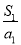 ,
,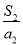 ,…,
,…, 中最大的项为( )
中最大的项为( )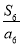 B.
B.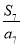 C.
C.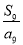 D.
D.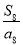
 的前n项和记为
的前n项和记为 ,
, ,则
,则 的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
 ;
; .
.