题目内容
(本小题满分12分)设数列 的前n项和为
的前n项和为 ,满足
,满足 ,且
,且 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若 成等差数列,求证:
成等差数列,求证: 成等差数列.
成等差数列.
(1)an=qn-1;(2)证明详见解析.
【解析】
试题分析:本题主要考查等比数列的通项公式及前n项和公式、等差中项等基础知识,意在考查考生的分析问题解决问题的能力、运算求解能力.第一问,当 时,代入到已知等式中可直接求出
时,代入到已知等式中可直接求出 的值,当
的值,当 时,利用
时,利用 ,得到
,得到 与
与 的关系,从而得出数列
的关系,从而得出数列 为等比数列,从而得到数列的通项公式;第二问,利用等比数列的前n项和公式,利用等差中项列出等式,通过约分,化简,得到a3+a6=2a9,再同时除以q,即得到结论.
为等比数列,从而得到数列的通项公式;第二问,利用等比数列的前n项和公式,利用等差中项列出等式,通过约分,化简,得到a3+a6=2a9,再同时除以q,即得到结论.
试题解析:(Ⅰ)当n=1时,由(1-q)S1+qa1=1,a1=1.
当n≥2时,由(1-q)Sn+qan=1,得(1-q)Sn-1+qan-1=1,两式相减得an=qan-1,
又q(q-1)≠0,所以{an}是以1为首项,q为公比的等比数列,
故an=qn-1. 6分
(Ⅱ)由(Ⅰ)可知 ,又S3+S6=2S9,得
,又S3+S6=2S9,得 ,
,
化简得a3+a6=2a9,两边同除以q得a2+a5=2a8.
故a2,a8,a5成等差数列. 12分
考点:等比数列的通项公式及前n项和公式、等差中项.
考点分析: 考点1:等差数列 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
 ;
; .
.
 B.
B. C.
C. D.
D.
 的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
 ;
; .
.
 B.
B. C.4 D.
C.4 D.

 B.
B. C.
C. D.
D.
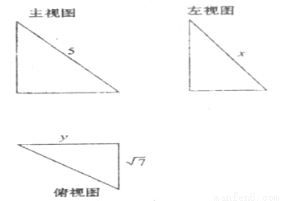
 ,则该锥体的俯视图可以是( )
,则该锥体的俯视图可以是( )

 ,若方程
,若方程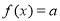 有四个不同的解
有四个不同的解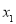 ,
,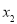 ,
, ,
,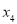 ,且
,且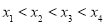 ,则
,则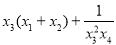 的取值范围是( )
的取值范围是( )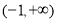 B.
B.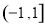 C.
C.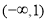 D.
D.