题目内容
设i为虚数单位,则(
)2014等于( )
| 1+i |
| i |
| A、21007i |
| B、-21007i |
| C、22014 |
| D、-22014 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:由复数代数形式的乘除运算化简
,然后利用虚数单位i的运算性质化简求值.
| 1+i |
| i |
解答:
解:∵(
)2=-2i,
∴(
)2014=(-2i)1007=(-2)1007•i1007=21007i.
故选:A.
| 1+i |
| i |
∴(
| 1+i |
| i |
故选:A.
点评:本题考查了复数代数形式的乘除运算,考查了虚数单位i的运算性质,是基础题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
a3>8是a>2的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |
已知命题p:存在x0∈R,使sinx0=1;命题q:x2=4的解集是{x|x=2},下列结论:
①命题“p∧q”是真命题;
②命题“p∧(¬q)”是真命题;
③命题“(¬p)∨q”是假命题;
④命题“(¬p)∨(¬q)”是假命题.
其中正确的是( )
①命题“p∧q”是真命题;
②命题“p∧(¬q)”是真命题;
③命题“(¬p)∨q”是假命题;
④命题“(¬p)∨(¬q)”是假命题.
其中正确的是( )
| A、②④ | B、②③ | C、①② | D、①③ |
已知复数z的共轭复数是
,则复数z3+2z2+
+1等于( )
| 2-2i |
| 1+i |
. |
| z |
| A、8+2i | B、5+3i |
| C、-7-10i | D、9-10i |
图中阴影部分所表示的集合是( )


| A、B∩[∁U(A∪C)] |
| B、(B∪C)∩(∁UA) |
| C、(A∪C)∩(∁UB) |
| D、(∁UA)∩B |
若集合M={x|2-x<0},N={x|x-3≤0},则M∩N为( )
| A、(-∞,-1)∪(2,3] |
| B、(-∞,3] |
| C、(2,3] |
| D、(1,3] |
 如图是2012年举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和中位数分别为( )
如图是2012年举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和中位数分别为( )| A、85,84 |
| B、85,84.5 |
| C、85,85 |
| D、85,85.5 |
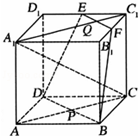 如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q;
如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q;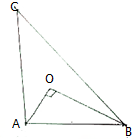 如图所示,已知点O为△ABC的重心,OA⊥OB,AB=6,则
如图所示,已知点O为△ABC的重心,OA⊥OB,AB=6,则