题目内容
求抛物线y=x2的过点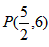
的切线方程。
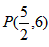的切线方程。解：设此切线过抛物线上的点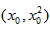
，由导数的意义知此切线的斜率为2x0，
又因为此切线过点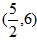
和点（x0，x02），其斜率应满足
，
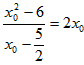由此x0应满足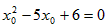
，解得x0=2或3，
即切线过抛物线y=x2上的点为（2，4）或（3，9），
所以切线方程为y-4=4（x-2）或y-9=6（x-3），
化简得y=4x-4或y=6x-9，此即是所求的切线方程。
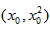，由导数的意义知此切线的斜率为2x0，又因为此切线过点
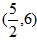和点（x0，x02），其斜率应满足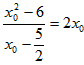，由此x0应满足
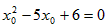，解得x0=2或3，即切线过抛物线y=x2上的点为（2，4）或（3，9），
所以切线方程为y-4=4（x-2）或y-9=6（x-3），
化简得y=4x-4或y=6x-9，此即是所求的切线方程。
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
过抛物线y=x2的顶点作互相垂直的两条弦OA、OB，抛物线的顶点O在直线AB上的射影为P，求动点P的轨迹方程．
x2的焦点，离心率等于
.
=λ1
，
=λ2
，求证λ1+λ2为定值.
x2上的点，过点Bn（n，bn）作抛物线y=
x2的切线交x轴于点An（an，0），点Cn（cn，0）在x轴上，且点An，Bn，Cn构成以点Bn为顶点的等腰三角形．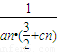
}的前n项和为Sn，求证：
≤Sn＜
．