题目内容
已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点恰好是抛物线y=
x2的焦点，离心率等于
.
求椭圆C的方程；
过椭圆C的右焦点F作直线l交椭圆C于A、B两点，交y轴于M点，若
=λ1
，
=λ2
，求证λ1+λ2为定值.
【小题1】设椭圆C的方程为
，则由题意知b = 1.
∴椭圆C的方程为 
…………………………………………………5分
【小题2】方法一：设A、B、M点的坐标分别为
易知F点的坐标为（2，0）.
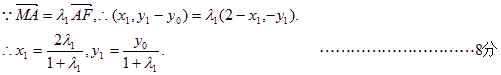
将A点坐标代入到椭圆方程中，得
去分母整理得
…………………………………………10分
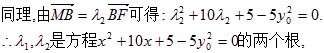
…………………………………………………………12分
方法二：设A、B、M点的坐标分别为又易知F点的坐标为（2，0）.
显然直线l存在的斜率，设直线l的斜率为k，则直线l的方程是
将直线l的方程代入到椭圆C的方程中，消去y并整理得
……………………………………7分
……………………………………8分
又
解析:
同答案
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
。