ΧβΡΩΡΎ»ί
“―÷ΣΒψΝ–B1Θ®1Θ§b1Θ©Θ§B2Θ®2Θ§b2Θ©Θ§Γ≠Θ§BnΘ®nΘ§bnΘ©Θ§Γ≠Θ®nΓ N?Θ©Υ≥¥ΈΈΣ≈ΉΈοœΏy= x2…œΒΡΒψΘ§ΙΐΒψBnΘ®nΘ§bnΘ©Ής≈ΉΈοœΏy=
x2…œΒΡΒψΘ§ΙΐΒψBnΘ®nΘ§bnΘ©Ής≈ΉΈοœΏy= x2ΒΡ«–œΏΫΜx÷α”ΎΒψAnΘ®anΘ§0Θ©Θ§ΒψCnΘ®cnΘ§0Θ©‘Ύx÷α…œΘ§«“ΒψAnΘ§BnΘ§CnΙΙ≥…“‘ΒψBnΈΣΕΞΒψΒΡΒ»―ϋ»ΐΫ«–ΈΘ°
x2ΒΡ«–œΏΫΜx÷α”ΎΒψAnΘ®anΘ§0Θ©Θ§ΒψCnΘ®cnΘ§0Θ©‘Ύx÷α…œΘ§«“ΒψAnΘ§BnΘ§CnΙΙ≥…“‘ΒψBnΈΣΕΞΒψΒΡΒ»―ϋ»ΐΫ«–ΈΘ°Θ®1Θ©«σ ΐΝ–{an}Θ§{cn}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύn ΙΒ»―ϋ»ΐΫ«–ΈAnBnCnΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§»τ”–Θ§«κ«σ≥ωnΘΜ»τΟΜ”–Θ§«κΥΒΟςάμ”…Θ°
Θ®3Θ©…η ΐΝ–{
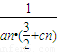 }ΒΡ«ΑnœνΚΆΈΣSnΘ§«σ÷ΛΘΚ
}ΒΡ«ΑnœνΚΆΈΣSnΘ§«σ÷ΛΘΚ ΓήSnΘΦ
ΓήSnΘΦ Θ°
Θ°
ΓΨ¥πΑΗΓΩΖ÷ΈωΘΚΘ®1Θ©άϊ”ΟΒΦ ΐΘ§«σΒΟΒψBnΘ®nΘ§bnΘ©Ής≈ΉΈοœΏy= x2ΒΡ«–œΏΖΫ≥ΧΘ§Ννy=0Θ§Ω…ΒΟan=
x2ΒΡ«–œΏΖΫ≥ΧΘ§Ννy=0Θ§Ω…ΒΟan= Θ§ΗυΨίΒψAnΘ§BnΘ§CnΙΙ≥…“‘ΒψBnΈΣΕΞΒψΒΡΒ»―ϋ»ΐΫ«–ΈΘ§Ω…ΒΟan+cn=2nΘ§”…¥ΥΩ…«σ ΐΝ–{an}Θ§{cn}ΒΡΆ®œνΙΪ ΫΘΜ
Θ§ΗυΨίΒψAnΘ§BnΘ§CnΙΙ≥…“‘ΒψBnΈΣΕΞΒψΒΡΒ»―ϋ»ΐΫ«–ΈΘ§Ω…ΒΟan+cn=2nΘ§”…¥ΥΩ…«σ ΐΝ–{an}Θ§{cn}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©»τΒ»―ϋ»ΐΫ«–ΈAnBnCnΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ|AnCn|=2bnΘ§”…¥ΥΩ…÷Σ¥φ‘Ύn=2Θ§ ΙΒ»―ϋ»ΐΫ«–ΈA2B2C2ΈΣ÷±Ϋ«»ΐΫ«–ΈΘΜ
Θ®3Θ© =
= =
= =
= Θ®
Θ® -
- Θ©Θ§¥”ΕχΩ…«σSn=
Θ©Θ§¥”ΕχΩ…«σSn= Θ®1-
Θ®1- Θ©Θ§ΫχΕχΩ…÷Σ
Θ©Θ§ΫχΕχΩ…÷Σ ΓήSnΘΦ
ΓήSnΘΦ Θ°
Θ°
Ϋβ¥πΘΚΘ®1Θ©ΫβΘΚΓΏy= x2Θ§ΓύyΓδ=
x2Θ§ΓύyΓδ= Θ§yΓδ|x=n=
Θ§yΓδ|x=n= Θ§
Θ§
ΓύΒψBnΘ®nΘ§bnΘ©Ής≈ΉΈοœΏy= x2ΒΡ«–œΏΖΫ≥ΧΈΣΘΚy-
x2ΒΡ«–œΏΖΫ≥ΧΈΣΘΚy- =
= Θ®x-nΘ©Θ§
Θ®x-nΘ©Θ§
Ννy=0Θ§‘ρx= Θ§Φ¥an=
Θ§Φ¥an= ΘΜΘ®3Ζ÷Θ©
ΘΜΘ®3Ζ÷Θ©
ΓΏΒψAnΘ§BnΘ§CnΙΙ≥…“‘ΒψBnΈΣΕΞΒψΒΡΒ»―ϋ»ΐΫ«–ΈΘ§
Γύan+cn=2nΘ§Γύcn=2n-an= Θ®5Ζ÷Θ©
Θ®5Ζ÷Θ©
Θ®2Θ©ΫβΘΚ»τΒ»―ϋ»ΐΫ«–ΈAnBnCnΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ|AnCn|=2bn?
Γύn= Θ§Γύn=2Θ§
Θ§Γύn=2Θ§
Γύ¥φ‘Ύn=2Θ§ ΙΒ»―ϋ»ΐΫ«–ΈA2B2C2ΈΣ÷±Ϋ«»ΐΫ«–Έ Θ®9Ζ÷Θ©
Θ®3Θ©÷ΛΟςΘΚΓΏ =
= =
= =
= Θ®
Θ® -
- Θ©Θ®11Ζ÷Θ©
Θ©Θ®11Ζ÷Θ©
ΓύSn= Θ®1-
Θ®1- +
+ -
- +Γ≠+
+Γ≠+ -
- Θ©=
Θ©= Θ®1-
Θ®1- Θ©ΘΦ
Θ©ΘΦ
”÷1- ΥφnΒΡ‘ω¥σΕχ‘ω¥σΘ§
ΥφnΒΡ‘ω¥σΕχ‘ω¥σΘ§
ΓύΒ±n=1 ±Θ§SnΒΡΉν–Γ÷ΒΈΣΘΚ Θ®1-
Θ®1- Θ©=
Θ©= Θ§
Θ§
Γύ ΓήSnΘΦ
ΓήSnΘΦ Θ®14Ζ÷Θ©
Θ®14Ζ÷Θ©
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΒΦ ΐΒΡΦΗΚΈ“β“εΘ§ΩΦ≤ιΝ―œνΖ®«σ ΐΝ–ΒΡΚΆΘ§ΩΦ≤ι≤ΜΒ» ΫΒΡ÷ΛΟςΘ§ΩΦ≤ι ΐΝ–”κΫβΈωΦΗΚΈΒΡΉέΚœΘ§ τ”Ύ÷–ΒΒΧβΘ°
 x2ΒΡ«–œΏΖΫ≥ΧΘ§Ννy=0Θ§Ω…ΒΟan=
x2ΒΡ«–œΏΖΫ≥ΧΘ§Ννy=0Θ§Ω…ΒΟan= Θ§ΗυΨίΒψAnΘ§BnΘ§CnΙΙ≥…“‘ΒψBnΈΣΕΞΒψΒΡΒ»―ϋ»ΐΫ«–ΈΘ§Ω…ΒΟan+cn=2nΘ§”…¥ΥΩ…«σ ΐΝ–{an}Θ§{cn}ΒΡΆ®œνΙΪ ΫΘΜ
Θ§ΗυΨίΒψAnΘ§BnΘ§CnΙΙ≥…“‘ΒψBnΈΣΕΞΒψΒΡΒ»―ϋ»ΐΫ«–ΈΘ§Ω…ΒΟan+cn=2nΘ§”…¥ΥΩ…«σ ΐΝ–{an}Θ§{cn}ΒΡΆ®œνΙΪ ΫΘΜΘ®2Θ©»τΒ»―ϋ»ΐΫ«–ΈAnBnCnΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ|AnCn|=2bnΘ§”…¥ΥΩ…÷Σ¥φ‘Ύn=2Θ§ ΙΒ»―ϋ»ΐΫ«–ΈA2B2C2ΈΣ÷±Ϋ«»ΐΫ«–ΈΘΜ
Θ®3Θ©
 =
= =
= =
= Θ®
Θ® -
- Θ©Θ§¥”ΕχΩ…«σSn=
Θ©Θ§¥”ΕχΩ…«σSn= Θ®1-
Θ®1- Θ©Θ§ΫχΕχΩ…÷Σ
Θ©Θ§ΫχΕχΩ…÷Σ ΓήSnΘΦ
ΓήSnΘΦ Θ°
Θ°Ϋβ¥πΘΚΘ®1Θ©ΫβΘΚΓΏy=
 x2Θ§ΓύyΓδ=
x2Θ§ΓύyΓδ= Θ§yΓδ|x=n=
Θ§yΓδ|x=n= Θ§
Θ§ΓύΒψBnΘ®nΘ§bnΘ©Ής≈ΉΈοœΏy=
 x2ΒΡ«–œΏΖΫ≥ΧΈΣΘΚy-
x2ΒΡ«–œΏΖΫ≥ΧΈΣΘΚy- =
= Θ®x-nΘ©Θ§
Θ®x-nΘ©Θ§Ννy=0Θ§‘ρx=
 Θ§Φ¥an=
Θ§Φ¥an= ΘΜΘ®3Ζ÷Θ©
ΘΜΘ®3Ζ÷Θ©ΓΏΒψAnΘ§BnΘ§CnΙΙ≥…“‘ΒψBnΈΣΕΞΒψΒΡΒ»―ϋ»ΐΫ«–ΈΘ§
Γύan+cn=2nΘ§Γύcn=2n-an=
 Θ®5Ζ÷Θ©
Θ®5Ζ÷Θ©Θ®2Θ©ΫβΘΚ»τΒ»―ϋ»ΐΫ«–ΈAnBnCnΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ|AnCn|=2bn?
Γύn=
 Θ§Γύn=2Θ§
Θ§Γύn=2Θ§Γύ¥φ‘Ύn=2Θ§ ΙΒ»―ϋ»ΐΫ«–ΈA2B2C2ΈΣ÷±Ϋ«»ΐΫ«–Έ Θ®9Ζ÷Θ©
Θ®3Θ©÷ΛΟςΘΚΓΏ
 =
= =
= =
= Θ®
Θ® -
- Θ©Θ®11Ζ÷Θ©
Θ©Θ®11Ζ÷Θ©ΓύSn=
 Θ®1-
Θ®1- +
+ -
- +Γ≠+
+Γ≠+ -
- Θ©=
Θ©= Θ®1-
Θ®1- Θ©ΘΦ
Θ©ΘΦ
”÷1-
 ΥφnΒΡ‘ω¥σΕχ‘ω¥σΘ§
ΥφnΒΡ‘ω¥σΕχ‘ω¥σΘ§ΓύΒ±n=1 ±Θ§SnΒΡΉν–Γ÷ΒΈΣΘΚ
 Θ®1-
Θ®1- Θ©=
Θ©= Θ§
Θ§Γύ
 ΓήSnΘΦ
ΓήSnΘΦ Θ®14Ζ÷Θ©
Θ®14Ζ÷Θ©ΒψΤάΘΚ±ΨΧβΩΦ≤ιΒΦ ΐΒΡΦΗΚΈ“β“εΘ§ΩΦ≤ιΝ―œνΖ®«σ ΐΝ–ΒΡΚΆΘ§ΩΦ≤ι≤ΜΒ» ΫΒΡ÷ΛΟςΘ§ΩΦ≤ι ΐΝ–”κΫβΈωΦΗΚΈΒΡΉέΚœΘ§ τ”Ύ÷–ΒΒΧβΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ Θ©1005-1]Θ©
Θ©1005-1]Θ© Θ©1005-1]Θ©
Θ©1005-1]Θ© Θ©2010-1]Θ©
Θ©2010-1]Θ© Θ©2010-1]Θ©
Θ©2010-1]Θ© BΘ°
BΘ°
 DΘ°
DΘ°