题目内容
 已知经过点P(0,2)且以
已知经过点P(0,2)且以| d |
(1)求实数a的取值范围;
(2)若点A、B均在已知双曲线的右支上,且满足
| OA |
| OB |
(3)是否存在这样的实数a,使得A、B两点关于直线y=
| 1 |
| 2 |
分析:(1)因为直线l经过点P(0,2)且以
=(1,a)为一个方向向量,所以可写出点斜式方程,与双曲线方程联立,因为直线与双曲线相交于不同两点,利用韦达定理,即可求出实数a的取值范围.
(2)若点A、B均在已知双曲线的右支上,则(1)中直线与双曲线联立得到的关于x的一元二次方程有两正根,除满足△≥0外,还需满足两根之和大于0,两根之积大于0,把a的范围进一步缩小,再由
•
=0,求出a值.
(3)先假设存在实数a,使得A、B两点关于直线y=
x-8对称,则直线y=
x-8为线段AB的垂直平分线,直线l的法向量与直线y=
x-8的法向量互相垂直,得到a的值,再求出直线l的方程,与双曲线方程联立,求出A,B点的中点M坐标,判断M点是否再直线y=
x-8,若在,则假设成立,否则,假设不成立.
| d |
(2)若点A、B均在已知双曲线的右支上,则(1)中直线与双曲线联立得到的关于x的一元二次方程有两正根,除满足△≥0外,还需满足两根之和大于0,两根之积大于0,把a的范围进一步缩小,再由
| OA |
| OB |
(3)先假设存在实数a,使得A、B两点关于直线y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)由已知,直线l的方程为 y=ax+2.
由
消去y,并整理得 (3-a2)x2-4ax-5=0.①
依题意得
解得 -
<a<
且a≠
且a≠-
.②
因此 所求的实数a的取值范围为 (-
,-
)∪(-
,
)∪(
,
).
(2)设A(x1,y1),B(x2,y2).因为点A、B均在已知双曲线的右支上,
所以 (1)中方程①具有两个不同的正实数根x1、x2,即x1>0、x2>0,
于是
解得 -
<a<-
.
又
•
=0,即 (x1,y1)•(x2,y2)=0,即 x1x2+y1y2=0,
而 y1y2=(ax1+2)(ax2+2)=a2x1x2+2a(x1+x2)+4,
所以 x1x2+a2x1x2+2a(x1+x2)+4=0,即 (1+a2)x1x2+2a(x1+x2)+4=0,
则 (1+a2)•(-
)+2a•
+4=0,解得 a=±
.
又因为 -
<a<-
,所以 a=-
.
因此 所求实数a的值为 -
.
(3)假设存在实数a,使A、B两点关于直线y=
x-8对称,则直线y=ax+2与y=
x-8相互垂直.
因为直线y=ax+1与y=
x-8的一个法向量分别为为(a,-1)、(1,-2),由题意,向量(a,-1)、(1,-2)也相互垂直,即有 (a,-1)•(1,-2)=0,即 a+2=0,解得a=-2.(注:由直线y=ax+2与y=
x-8相互垂直得 a•
=-1,解得a=-2.这样做也行.)
所以直线l的方程为y=-2x+2.
联立方程组
消去y,并整理得 x2-8x+5=0.
这里△=(-8)2-20=44>0,且x1+x2=8,x1x2=-5,
所以
=4,则
=-2•(
)+2=-6.
设线段AB的中点为M,则 M(4,-6).
由于AB中点M(4,-6)也在直线y=
x-8上,
因此 存在实a=-2,可使A、B两点关于直线y=
x-8对称.
由
|
依题意得
|
| 15 |
| 15 |
| 3 |
| 3 |
因此 所求的实数a的取值范围为 (-
| 15 |
| 3 |
| 3 |
| 3 |
| 3 |
| 15 |
(2)设A(x1,y1),B(x2,y2).因为点A、B均在已知双曲线的右支上,
所以 (1)中方程①具有两个不同的正实数根x1、x2,即x1>0、x2>0,
于是
|
| 13 |
| 3 |
又
| OA |
| OB |
而 y1y2=(ax1+2)(ax2+2)=a2x1x2+2a(x1+x2)+4,
所以 x1x2+a2x1x2+2a(x1+x2)+4=0,即 (1+a2)x1x2+2a(x1+x2)+4=0,
则 (1+a2)•(-
| 5 |
| 3-a2 |
| 4a |
| 3-a2 |
| 7 |
又因为 -
| 13 |
| 3 |
| 7 |
因此 所求实数a的值为 -
| 7 |
(3)假设存在实数a,使A、B两点关于直线y=
| 1 |
| 2 |
| 1 |
| 2 |
因为直线y=ax+1与y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以直线l的方程为y=-2x+2.
联立方程组
|
这里△=(-8)2-20=44>0,且x1+x2=8,x1x2=-5,
所以
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
设线段AB的中点为M,则 M(4,-6).
由于AB中点M(4,-6)也在直线y=
| 1 |
| 2 |
因此 存在实a=-2,可使A、B两点关于直线y=
| 1 |
| 2 |
点评:本题主要考查了韦达定理在直线与双曲线位置关系判断中的应用,注意设而不求思想的应用.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 已知经过点P(0,2)且以
已知经过点P(0,2)且以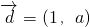 为一个方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B.
为一个方向向量的直线l与双曲线3x2-y2=1相交于不同两点A、B. ,求实数a的值;
,求实数a的值; 对称?若存在,请求出a的值;若不存在,请说明理由.
对称?若存在,请求出a的值;若不存在,请说明理由.