题目内容
已知过点P(0,2)的直线l与抛物线C:y2=4x交于A、B两点,O为坐标原点.(1)若以AB为直径的圆经过原点O,求直线l的方程;
(2)若线段AB的中垂线交x轴于点Q,求△POQ面积的取值范围.
【答案】分析:(1)设直线AB的方程为y=kx+2(k≠0),A(x1,y1),B(x2,y2),由 ,得k2x2+(4k-4)x+4=0,由△=(4k-4)2-16k2>0,得k<
,得k2x2+(4k-4)x+4=0,由△=(4k-4)2-16k2>0,得k< ,由
,由 =
= ,
, ,知y1y2=(kx1+2)(kx2+2)=
,知y1y2=(kx1+2)(kx2+2)= ,由以AB为直径的圆经过原点O,能求出直线l的方程.
,由以AB为直径的圆经过原点O,能求出直线l的方程.
(2)设线段AB的中点坐标为(x,y),由 ,得
,得 ,故线段AB的中垂线方程为
,故线段AB的中垂线方程为 ,由此能求出△POQ面积的取值范围.
,由此能求出△POQ面积的取值范围.
解答:解:(1)设直线AB的方程为y=kx+2(k≠0),
设A(x1,y1),B(x2,y2),
由 ,得k2x2+(4k-4)x+4=0,
,得k2x2+(4k-4)x+4=0,
则由△=(4k-4)2-16k2=-32k+16>0,得k< ,
,
 =
= ,
, ,
,
所以y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4= ,
,
因为以AB为直径的圆经过原点O,
所以∠AOB=90°,
即 ,
,
所以 ,
,
解得k=- ,
,
即所求直线l的方程为y=- .
.
(2)设线段AB的中点坐标为(x,y),
则由(1)得 ,
, ,
,
所以线段AB的中垂线方程为 ,
,
令y=0,得 =
= =
= ,
,
又由(1)知k< ,且k≠0,得
,且k≠0,得 或
或 ,
,
所以 ,
,
所以 =
= ,
,
所以△POQ面积的取值范围为(2,+∞).
点评:本题考查直线l的方程的求法和求△POQ面积的取值范围.考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
 ,得k2x2+(4k-4)x+4=0,由△=(4k-4)2-16k2>0,得k<
,得k2x2+(4k-4)x+4=0,由△=(4k-4)2-16k2>0,得k< ,由
,由 =
= ,
, ,知y1y2=(kx1+2)(kx2+2)=
,知y1y2=(kx1+2)(kx2+2)= ,由以AB为直径的圆经过原点O,能求出直线l的方程.
,由以AB为直径的圆经过原点O,能求出直线l的方程.(2)设线段AB的中点坐标为(x,y),由
 ,得
,得 ,故线段AB的中垂线方程为
,故线段AB的中垂线方程为 ,由此能求出△POQ面积的取值范围.
,由此能求出△POQ面积的取值范围.解答:解:(1)设直线AB的方程为y=kx+2(k≠0),
设A(x1,y1),B(x2,y2),
由
 ,得k2x2+(4k-4)x+4=0,
,得k2x2+(4k-4)x+4=0,则由△=(4k-4)2-16k2=-32k+16>0,得k<
 ,
, =
= ,
, ,
,所以y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=
 ,
,因为以AB为直径的圆经过原点O,
所以∠AOB=90°,
即
 ,
,所以
 ,
,解得k=-
 ,
,即所求直线l的方程为y=-
 .
.(2)设线段AB的中点坐标为(x,y),
则由(1)得
 ,
, ,
,所以线段AB的中垂线方程为
 ,
,令y=0,得
 =
= =
= ,
,又由(1)知k<
 ,且k≠0,得
,且k≠0,得 或
或 ,
,所以
 ,
,所以
 =
= ,
,所以△POQ面积的取值范围为(2,+∞).
点评:本题考查直线l的方程的求法和求△POQ面积的取值范围.考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目
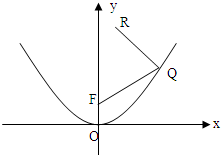 如图所示,F是抛物线x2=2py(p>0)的焦点,点R(1,4)为抛物线内一定点,点Q为抛物线上一动点,|QR|+|QF|的最小值为5.
如图所示,F是抛物线x2=2py(p>0)的焦点,点R(1,4)为抛物线内一定点,点Q为抛物线上一动点,|QR|+|QF|的最小值为5.