题目内容
【题目】已知函数![]() ,函数
,函数![]() 是函数
是函数![]() 的反函数.
的反函数.
![]() 求函数
求函数![]() 的解析式,并写出定义域
的解析式,并写出定义域![]() ;
;
![]() 设
设![]() ,判断并证明函数
,判断并证明函数![]() 在区间
在区间![]() 上的单调性:
上的单调性:
![]() 若
若![]() 中的函数
中的函数![]() 在区间
在区间![]() 内的图像是不间断的光滑曲线,求证:函数
内的图像是不间断的光滑曲线,求证:函数![]() 在区间
在区间![]() 内必有唯一的零点(假设为
内必有唯一的零点(假设为![]() ),且
),且![]() .
.
【答案】(1)![]() ;
;![]() ;
;
(2)![]() 在区间
在区间![]() 上是减函数,证明见解析;
上是减函数,证明见解析;
(3)证明见解析.
【解析】
(1)根据![]() 和
和![]() 得出
得出![]() ,此范围就是其反函数的定义域,再由
,此范围就是其反函数的定义域,再由![]() ,可解得
,可解得![]() ,
,![]() ,再将
,再将![]() 互换得
互换得![]() ,从而得函数
,从而得函数![]() 的解析式;
的解析式;
(2)设![]() ,则
,则![]() ,
,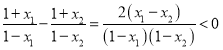 ,
,![]() ,可得
,可得![]() ,可得证;
,可得证;
(3)先判断函数![]() 的奇偶性,再由(2)得出
的奇偶性,再由(2)得出![]() 在上
在上![]() 的单调性,根据零点存在定理可得证.
的单调性,根据零点存在定理可得证.
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]()
由![]() ,得
,得![]() ,
,![]() ,
,![]() 互换得
互换得![]() ,
,
![]() ,定义域
,定义域![]()
![]()
![]() 在区间
在区间![]() 上的单调递减,证明如下:
上的单调递减,证明如下:
由(1)可知,![]() ,且定义域为
,且定义域为![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,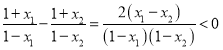
![]() ,
,
![]()
![]()
由![]() 得
得![]() ,即
,即![]() ,
,
![]() 在区间
在区间![]() 上是减函数;
上是减函数;
![]() 对任意
对任意![]() ,有
,有![]() ,
,
所以,函数![]() 是奇函数,
是奇函数,
由(2)得![]() 在区间
在区间![]() 上是减函数,所以函数
上是减函数,所以函数![]() 在
在![]() 上单调递减,且在
上单调递减,且在![]() 上的图像也是不间断的光滑曲线,
上的图像也是不间断的光滑曲线,
又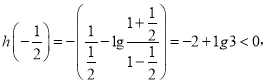
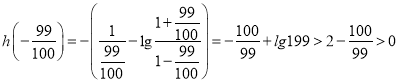 ,
,
所以![]() ,根据零点存在定理得:函数
,根据零点存在定理得:函数![]() 在区间
在区间![]() 上有且仅有唯一零点,
上有且仅有唯一零点,
所以,函数![]() 在区间
在区间![]() 上有且仅有唯一零点
上有且仅有唯一零点![]() ,且
,且![]() .
.
故得解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


