题目内容
【题目】已知
件次品和
件正品混放在一起，现需要通过检测将其区分，每次随机检测一件产品，检测后不放回，直到检测出件次品或者检测出件正品时检测结束．
（1）求第一次检测出的是次品且第二次检测出的是正品的概率；
（2）已知每检测一件产品需要费用
元，设
表示直到检测出件次品或者检测出件正品时所需要的检测费用（单位：元），求的分布列．
【答案】（1）
；（2）见解析.
【解析】
（1）利用独立事件的概率乘法公式可计算出所求事件的概率；
（2）由题意可知随机变量
的可能取值有
、
、
，计算出随机变量在不同取值下的概率，由此可得出随机变量的分布列.
（1）记“第一次检测出的是次品且第二次检测出的是正品”为事件
，则
；
（2）由题意可知，随机变量的可能取值为、、．
则
，
，
．
故的分布列为
|
|
|
|
|
|
|
|
练习册系列答案
相关题目
【题目】我国全面二孩政策已于2016年1月1日起正式实施．国家统计局发布的数据显示，从2012年到2017年，中国的人口自然增长率变化始终不大，在5‰上下波动（如图）．
为了了解年龄介于24岁至50岁之间的适孕夫妻对生育二孩的态度如何，统计部门按年龄分为9组，每组选取150对夫妻进行调查统计有生育二孩意愿的夫妻数，得到下表：
年龄区间 |
|
|
|
|
|
|
|
|
|
有意愿数 | 80 | 81 | 87 | 86 | 84 | 83 | 83 | 70 | 66 |
（1）设每个年龄区间的中间值为
，有意愿数为
，求样本数据的线性回归直线方程，并求该模型的相关系数
（结果保留两位小数）；
（2）从
，
，
，
，
这五个年龄段中各选出一对夫妻（能代表该年龄段超过半数夫妻的意愿）进一步调研，再从这5对夫妻中任选2对夫妻．求其中恰有一对不愿意生育二孩的夫妻的概率．
（参考数据和公式：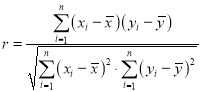
，
，
，
，
，
）
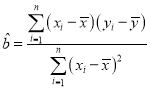