题目内容
(
湖南长郡中学模拟)如下图,四棱锥P—ABCD的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,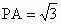 ,E为PC的中点.
,E为PC的中点.
(1)
求直线DE与平面PAC所成角的大小;(2)
在线段PC上是否存在一点M,使PC⊥平面MBD成立.请说明理由.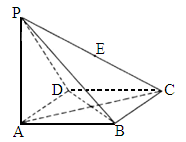
答案:略
解析:
解析:
|
解析: (1)如图,连AC、BD,则由PA⊥底面ABCD,得平面PAC⊥底面ABCD于AC,又由底面ABCD为菱形可得BD⊥AC于O,∴DO⊥平面PAC.连 OE,则OE为DE在平面PAC的射影,∴∠ DEO即为DE与平面PAC所成的角.由 E为PC的中点可得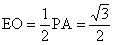 . .
又由菱形的性质可得, Rt△AOD中,∠ADO=60°,AD=1,∴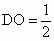 . .
∴在 Rt△DEO中, , ,
∴∠ DEO=30°. (6分)
(2) 设AC∩BD=O,过O作OM⊥PC于M,则由PA⊥底面ABCD,可得平面PAC⊥底面ABCD于AC.又BD⊥PC,BD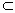 底面ABCD,∴BD⊥平面PAC,∴BD⊥PC,而由OM 底面ABCD,∴BD⊥平面PAC,∴BD⊥PC,而由OM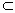 平面PAC且OM⊥PC,可得PC⊥平面MBD.故在线段PC上存在一点M,使PC⊥平面MBD成立. 平面PAC且OM⊥PC,可得PC⊥平面MBD.故在线段PC上存在一点M,使PC⊥平面MBD成立.
(12 分) |

练习册系列答案
相关题目


 、
、 分别为双曲线的左、右焦点,P是双曲线
分别为双曲线的左、右焦点,P是双曲线 左支上的一点,若
左支上的一点,若 ,则双曲线的离心率取值范围是______.
,则双曲线的离心率取值范围是______. (-3,0),
(-3,0), (3,0),则椭圆的方程为________.
(3,0),则椭圆的方程为________. 相切.过点P(-4,0)作斜率为
相切.过点P(-4,0)作斜率为 的直线l,使得l和G交于A,B两点,和y轴交于点C,并且点P在线段AB上,又满足
的直线l,使得l和G交于A,B两点,和y轴交于点C,并且点P在线段AB上,又满足 .
.
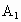 、
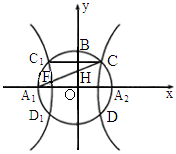
、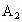 为焦点的双曲线E与半径为c的圆O相交于C、D、
为焦点的双曲线E与半径为c的圆O相交于C、D、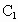 、
、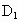 ,连接
,连接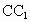 与OB交于点H,且有
与OB交于点H,且有 ,其中
,其中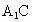 ,与双曲线E交于点F,是否存在实数λ,使
,与双曲线E交于点F,是否存在实数λ,使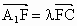 恒成立?若存在,试求出λ的值;若不存在,请说明理由.
恒成立?若存在,试求出λ的值;若不存在,请说明理由.