题目内容
8.执行如图所示的程序框图,如果输入n=4,则输出的S=( )
| A. | $\frac{5}{11}$ | B. | $\frac{3}{7}$ | C. | $\frac{8}{9}$ | D. | $\frac{4}{9}$ |
分析 由已知中的程序框图可知,该程序的功能是计算出输出S=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+$\frac{1}{7×9}$的值,利用裂项相消法,可得答案.
解答 解:由已知中的程序框图可知,
该程序的功能是计算并输出S=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+$\frac{1}{7×9}$的值,
由于:S=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+$\frac{1}{7×9}$=$\frac{1}{2}$×(1-$\frac{1}{3}+\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{7}$-$\frac{1}{9}$)=$\frac{1}{2}×$(1-$\frac{1}{9}$)=$\frac{4}{9}$.
故选:D.
点评 本题考查的知识点是程序框图,其中根据已知的程序框图分析出程序的功能是解答的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若a为实数,且$\frac{2-ai}{1+i}=3+i$,则a=( )
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
19.已知定义在[1,+∞)上的函数$f(x)=\left\{\begin{array}{l}4-8|{x-\frac{3}{2}}|,1≤x≤2\\ \frac{1}{2}f({\frac{x}{2}}),x>2\end{array}\right.$,当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的图象面积为Sn,则Sn=( )
| A. | n | B. | 2 | C. | 2n | D. | $\frac{n}{2}$ |
3.若执行如图所示的程序框图,输入x1=1,x2=2,x3=3,$\overline{x}$=2,则输出的数S等于( )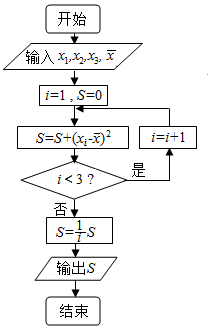

| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
13.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{1+9{x}^{2},}}&{x≤0}\\{1+x{e}^{x-1},}&{x>0}\end{array}\right.$,点A、B是函数f(x)图象上不同两点,则∠AOB(O为坐标原点)的取值范围是( )
| A. | (0,$\frac{π}{4}$) | B. | (0,$\frac{π}{4}$] | C. | (0,$\frac{π}{3}$) | D. | (0,$\frac{π}{3}$] |