题目内容
已知双曲线
-
=1,F1、F2为焦点.
(Ⅰ)若P为双曲线
-
=1上一点,且∠F1PF2=60°,求△F1PF2的面积;
(Ⅱ)若双曲线C与双曲线
-
=1有相同的渐近线,且过点M(-3
,5),求双曲线C的方程.
| y2 |
| 25 |
| x2 |
| 9 |
(Ⅰ)若P为双曲线
| y2 |
| 25 |
| x2 |
| 9 |
(Ⅱ)若双曲线C与双曲线
| y2 |
| 25 |
| x2 |
| 9 |
| 3 |
(Ⅰ)设|PF1|=r1,|PF2|=r2,则|r1-r2|=10①…(2分)
由余弦定理可得
+
-2r1r2•cos60°=(2
)2②,
①2-②得r1r2=36…(4分)
∴S△F1PF2=
r1r2sin60°=
×36×
=9
…(6分)
(Ⅱ)由已知可设双曲线C的方程为
-
=λ(λ≠0)…(8分)
将点M(-3
,5)坐标代入方程得:λ=
-
=-2…(10分)
∴双曲线C方程为:
-
=1…(12分)
由余弦定理可得
| r | 21 |
| r | 22 |
| 34 |
①2-②得r1r2=36…(4分)
∴S△F1PF2=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
(Ⅱ)由已知可设双曲线C的方程为
| y2 |
| 25 |
| x2 |
| 9 |
将点M(-3
| 3 |
| 52 |
| 25 |
| 27 |
| 9 |
∴双曲线C方程为:
| x2 |
| 18 |
| y2 |
| 50 |

练习册系列答案
相关题目
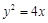 ,直线l过定点
,直线l过定点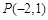 ,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?
,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点? 分别是椭圆
分别是椭圆 的左、右焦点,过点
的左、右焦点,过点 的直线交椭圆
的直线交椭圆 于
于 两点,若
两点,若 轴,则椭圆
轴,则椭圆