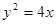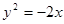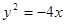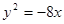题目内容
已知抛物线的方程为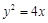 ,直线l过定点
,直线l过定点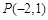 ,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?
,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?
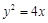 ,直线l过定点
,直线l过定点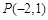 ,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?
,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?当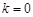 ,
, 或
或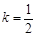 ,此时直线l与该抛物线只有一个公共点;当
,此时直线l与该抛物线只有一个公共点;当 ,此时直线l与该抛物线有两个公共点;当
,此时直线l与该抛物线有两个公共点;当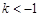 或
或 ,此时直线l与该抛物线没有公共点.
,此时直线l与该抛物线没有公共点.
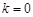 ,
, 或
或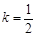 ,此时直线l与该抛物线只有一个公共点;当
,此时直线l与该抛物线只有一个公共点;当 ,此时直线l与该抛物线有两个公共点;当
,此时直线l与该抛物线有两个公共点;当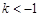 或
或 ,此时直线l与该抛物线没有公共点.
,此时直线l与该抛物线没有公共点.试题分析:解题思路:联立直线方程与抛物线方程,得到关于
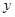 的一元二次方程,利用判别式的符号判定直线与抛物线的交点个数.规律总结:解决直线与圆锥曲线的交点个数,一般思路是联立直线与圆锥曲线的方程,整理得到关于
的一元二次方程,利用判别式的符号判定直线与抛物线的交点个数.规律总结:解决直线与圆锥曲线的交点个数,一般思路是联立直线与圆锥曲线的方程,整理得到关于 或
或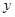 的一元二次方程,利用判别式的符号进行判定.注意点:当整理得到的一元二次方程的二次项系数为字母时,要注意讨论二次项系数是否为0.
的一元二次方程,利用判别式的符号进行判定.注意点:当整理得到的一元二次方程的二次项系数为字母时,要注意讨论二次项系数是否为0.试题解析:直线l的方程为
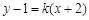 ,
,联立方程组
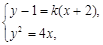 得
得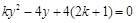 .
.①当
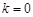 时,知方程有一个解,直线l与该抛物线只有一个公共点.
时,知方程有一个解,直线l与该抛物线只有一个公共点.②当
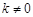 时,方程的判别式为
时,方程的判别式为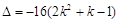 ,
,若
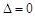 ,则
,则 或
或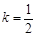 ,此时直线l与该抛物线只有一个公共点.
,此时直线l与该抛物线只有一个公共点.若
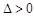 ,则
,则 ,此时直线l与该抛物线有两个公共点.
,此时直线l与该抛物线有两个公共点.若
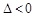 ,则
,则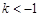 或
或 ,此时直线l与该抛物线没有公共点.
,此时直线l与该抛物线没有公共点.综上:当
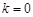 ,
, 或
或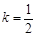 ,此时直线l与该抛物线只有一个公共点;
,此时直线l与该抛物线只有一个公共点;当
 ,此时直线l与该抛物线有两个公共点;
,此时直线l与该抛物线有两个公共点;当
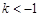 或
或 ,此时直线l与该抛物线没有公共点.
,此时直线l与该抛物线没有公共点.
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
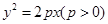 的焦点F,且交抛物线与A、B两点,若AB的中点到抛物线准线的距离1,则P的值为( ).
的焦点F,且交抛物线与A、B两点,若AB的中点到抛物线准线的距离1,则P的值为( ).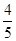 C.
C.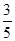 D.
D.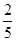
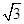 的直线与L相交于A,与C的一个交点为B,若
的直线与L相交于A,与C的一个交点为B,若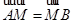 ,则p=____ 。
,则p=____ 。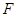 :
: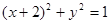 相外切,且与定直线
相外切,且与定直线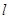 :
: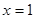 相切,则此动圆的圆心
相切,则此动圆的圆心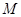 的轨迹方程是( )
的轨迹方程是( )