题目内容
已知![]() ,
,![]() ,
,![]() ,其中
,其中![]() 。
。
(I)若![]() 与
与![]() 的图像在交点(2,
的图像在交点(2,![]() )处的切线互相垂直,求
)处的切线互相垂直,求![]() 的值;
的值;
(II)若![]() 是函数
是函数![]() 的一个极值点,
的一个极值点,![]() 和1是
和1是![]() 的两个零点,且
的两个零点,且![]() ∈(
∈(![]()
![]() ,求
,求![]() ;
;
(III)当![]() 时,若
时,若![]() ,
,![]() 是
是![]() 的两个极值点,当|
的两个极值点,当|![]() -
-![]() |>1时,求证:|
|>1时,求证:|![]() -
-![]() |>3-4
|>3-4![]() 。
。
(I)![]() ,
,![]() …………………………1分
…………………………1分
由题知![]() ,即
,即![]() ……………………2分
……………………2分
解得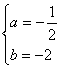
(II)![]() =
=![]() ,
,![]()
由题知![]() ,即
,即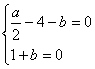 解得
解得![]() =6,
=6,![]() =-1……………………6分
=-1……………………6分
∴![]() =6
=6![]() -(
-(![]() -
-![]() ),
),![]() =
=![]()
∵![]() >0,由
>0,由![]() >0,解得0<
>0,解得0<![]() <2;由
<2;由![]() <0,解得
<0,解得![]() >2
>2
∴![]() 在(0,2)上单调递增,在(2,+∞)单调递减,
在(0,2)上单调递增,在(2,+∞)单调递减,
故![]() 至多有两个零点,其中
至多有两个零点,其中![]() ∈(0,2),
∈(0,2),![]() ∈(2, +∞)…………7分
∈(2, +∞)…………7分
又![]() >
>![]() =0,
=0,![]() =6(
=6(![]() -1)>0,
-1)>0,![]() =6(
=6(![]() -2)<0
-2)<0
∴![]() ∈(3,4),故
∈(3,4),故![]() =3 ……………………9分
=3 ……………………9分
(III)当![]() 时,
时,![]() =
=![]() ,
,
![]() =
=![]() ,
,
由题知![]() =0在(0,+∞)上有两个不同根
=0在(0,+∞)上有两个不同根![]() ,
,![]() ,则
,则![]() <0且
<0且![]() ≠-2,此时
≠-2,此时![]() =0的两根为-
=0的两根为-![]() ,1,……………………10分
,1,……………………10分
由题知|-![]() -1|>1,则
-1|>1,则![]() +
+![]() +1>1,
+1>1,![]() +4
+4![]() >0
>0
又∵![]() <0,∴
<0,∴![]() <-4,此时-
<-4,此时-![]() >1
>1
则![]() 与
与![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
|
| (0,1) | 1 | (1, - | - | (- |
|
| - | 0 | + | 0 | - |
|
|
| 极小值 |
| 极大值 |
|
∴|![]() -
-![]() |=
|=![]() 极大值-
极大值-![]() 极小值=F(-
极小值=F(-![]() )—F(1)
)—F(1)
=![]() —
—![]() )+
)+![]()
![]() —1,…………11分
—1,…………11分
设![]() ,则
,则![]()
,![]() ,∵
,∵![]() <-4,∴
<-4,∴![]() >—
>—![]() ,∴
,∴![]() >0,
>0,
∴![]() 在(—∞,—4)上是增函数,
在(—∞,—4)上是增函数,![]() <
<![]()
![]()
从而![]() 在(—∞,—4)上是减函数,∴
在(—∞,—4)上是减函数,∴![]() >
>![]() =3-4
=3-4![]()
所以|![]() -
-![]() |>3-4
|>3-4![]() 。
。

练习册系列答案
相关题目
