题目内容
(本题满分7分)已知命题:“ ,使等式
,使等式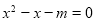 成立”是真命题.
成立”是真命题.
(1)求实数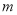 的取值集合
的取值集合 ; (5分)
; (5分)
(2)设不等式 的解集为
的解集为 ,若
,若 是
是 的必要条件,求
的必要条件,求 的取值范围.
的取值范围.
(1) (2)
(2) 或
或 .
.
【解析】
试题分析:命题:“ ,使等式
,使等式 成立”是真命题说明方程
成立”是真命题说明方程
在 上有实数解,则
上有实数解,则 在
在 有实数解,令
有实数解,令
 ,当
,当 时,
时, ,则
,则 ,从而得出集合
,从而得出集合 ,第二步解不等式
,第二步解不等式 需对
需对 进行讨论得出集合
进行讨论得出集合 ,最后根据
,最后根据 的要求,得出
的要求,得出 的取值范围.
的取值范围.
试题解析:(1)由题意知,方程 在
在 上有解,
上有解,
即 的取值范围就为函数
的取值范围就为函数 在
在 上的值域,易得
上的值域,易得 .
.
(2)因为 是
是 的必要条件,所以
的必要条件,所以
当 时,解集
时,解集 为空集,不满足题意
为空集,不满足题意
当 时,
时, ,此时集合
,此时集合
则 ,解得
,解得
当 时,
时, ,此时集合
,此时集合 ,
,
则
综上 或
或 .
.
考点:1.存在性命题的解题方法;2.充要条件;3.集合的包含关系的的处理方法;

练习册系列答案
相关题目
 及点
及点 .
. 为圆
为圆 上任一点,求
上任一点,求 的最大值和最小值;
的最大值和最小值; ,直线
,直线 与圆C交于点A、B, 当
与圆C交于点A、B, 当 为何值时
为何值时 取到最小值。
取到最小值。 B.
B. C.
C. D.
D.
 在定义域内可导,
在定义域内可导, 的图象如图,则导函数
的图象如图,则导函数 的图象可能为 ( )
的图象可能为 ( )

 ,
,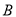 的坐标分别为
的坐标分别为 ,
,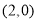 .直线
.直线 ,
, 相交于点
相交于点 ,且它们的斜率之积是
,且它们的斜率之积是 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线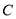 .
.  的方程;
的方程;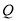 是曲线
是曲线 上的动点,直线
上的动点,直线 ,
, 分别交直线
分别交直线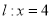 于点
于点 ,线段
,线段 的中点为
的中点为 ,求直线
,求直线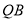 与直线
与直线 的斜率之积的取值范围;
的斜率之积的取值范围; 与
与 的交点为
的交点为 ,试探究点
,试探究点 的位置关系,并说明理由.
的位置关系,并说明理由. 的离心率为 .
的离心率为 . 在一个周期内的图象如图所示,则此函数的解析式是
在一个周期内的图象如图所示,则此函数的解析式是




 的单调减区间为 .
的单调减区间为 .