题目内容
(本小题14分)已知点 ,
,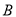 的坐标分别为
的坐标分别为 ,
,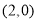 .直线
.直线 ,
, 相交于点
相交于点 ,且它们的斜率之积是
,且它们的斜率之积是 ,记动点
,记动点 的轨迹为曲线
的轨迹为曲线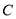 .
.
(1)求曲线 的方程;
的方程;
(2)设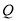 是曲线
是曲线 上的动点,直线
上的动点,直线 ,
, 分别交直线
分别交直线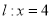 于点
于点 ,线段
,线段 的中点为
的中点为 ,求直线
,求直线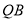 与直线
与直线 的斜率之积的取值范围;
的斜率之积的取值范围;
(3)在(2)的条件下,记直线 与
与 的交点为
的交点为 ,试探究点
,试探究点 与曲线
与曲线 的位置关系,并说明理由.
的位置关系,并说明理由.
(1)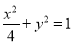 (
(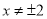 ),(2)
),(2)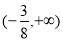 ,(3)点
,(3)点 在曲线
在曲线 上
上
【解析】
试题分析:首先设动点 ,利用直接法依据斜率之积等于
,利用直接法依据斜率之积等于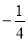 ,求出点
,求出点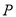 的轨迹方程,注意
的轨迹方程,注意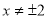 这个条件即可;第二步设直线
这个条件即可;第二步设直线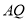 的斜率为
的斜率为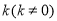 ,则由题可得直线
,则由题可得直线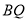 的斜率为
的斜率为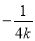 ,用点斜式写出
,用点斜式写出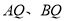 的方程,与
的方程,与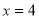 联立得出
联立得出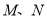 的坐标,得出
的坐标,得出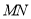 中点
中点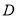 的坐标,最后写出
的坐标,最后写出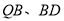 斜率之积求出范围即可;第三步由于
斜率之积求出范围即可;第三步由于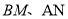 斜率之积为
斜率之积为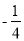 ,所以交点
,所以交点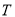 在曲线C上.
在曲线C上.
试题解析:(1)设动点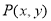 ,则
,则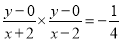 (
(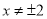 且
且 )
)
所以曲线 的方程为
的方程为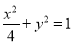 (
(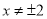 ).
).
(2)设直线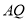 的斜率为
的斜率为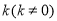 ,则由题可得直线
,则由题可得直线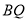 的斜率为
的斜率为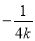 ,
,
所以直线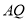 的方程为
的方程为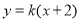 ,令
,令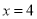 ,则得
,则得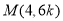 ,直线
,直线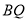 的方程为
的方程为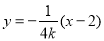 ,令
,令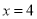 ,则得
,则得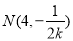 ,∴线段
,∴线段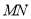 的中点
的中点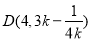 ,∴
,∴ 
故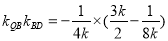
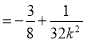
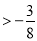 ∴直线
∴直线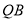 与直线
与直线 的斜率之积的取值范围为
的斜率之积的取值范围为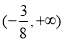
(3)由(2)得,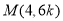 ,
,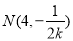 ,
,
∴ 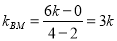 ,
,
∴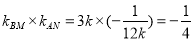 ∴ 点
∴ 点 在曲线
在曲线 上.
上.
考点:1.求轨迹方程;2.两条直线的交点;3.取值范围问题;

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 过圆
过圆 的圆心,则实数
的圆心,则实数 的值为( )
的值为( ) 1 B.1 C.3 D.
1 B.1 C.3 D.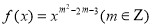 为偶函数,且在
为偶函数,且在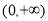 上是单调递减函数,则m的值为
上是单调递减函数,则m的值为 是椭圆
是椭圆 上的动点,
上的动点, 为椭圆的两个焦点,
为椭圆的两个焦点, 是原点,若
是原点,若 是
是 的角平分线上一点,且
的角平分线上一点,且 ,则
,则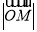 的取值范围是( )
的取值范围是( )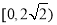 C.
C. D.[0,4]
D.[0,4] 的前n项和为
的前n项和为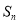 ,且4
,且4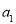 ,2
,2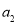 ,
,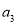 成等差数列。若
成等差数列。若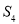 =( )
=( ) ,使等式
,使等式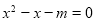 成立”是真命题.
成立”是真命题.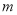 的取值集合
的取值集合 ; (5分)
; (5分) 的解集为
的解集为 ,若
,若 是
是 的必要条件,求
的必要条件,求 的取值范围.
的取值范围.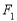 、
、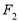 是双曲线
是双曲线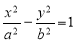
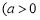 ,
,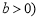 的左、右焦点,过
的左、右焦点,过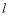 与双曲线的左、右两个分支分别交于点
与双曲线的左、右两个分支分别交于点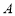 、
、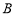 ,若
,若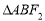 为等边三角形,则该双曲线的渐近线的斜率为( )
为等边三角形,则该双曲线的渐近线的斜率为( )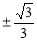 (B)
(B)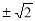 (C)
(C)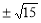 (D)
(D)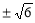
 上随机取一个数x,
上随机取一个数x, 的值介于0到
的值介于0到 之间的概率为 .
之间的概率为 .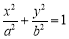
 的右焦点为
的右焦点为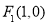 ,离心率为
,离心率为 .设A,B为椭圆上关于原点对称的两点,
.设A,B为椭圆上关于原点对称的两点, 的中点为M,
的中点为M, 的中点为N,原点
的中点为N,原点 在以线段
在以线段 为直径的圆上.设直线AB的斜率为k,若
为直径的圆上.设直线AB的斜率为k,若 ,则
,则