题目内容
已知点G是△ABO的重心,M是AB边的中点.且
=
,
=
,
=m
,
=n
,求证:
+
=3.
| OA |
| a |
| OB |
| b |
| OP |
| a |
| OQ |
| b |
| 1 |
| m |
| 1 |
| n |
分析:先确定
=
(
+
),
=
(
+
),根据PQ过△ABO的重心G,可得
=λ
,利用平面向量基本定理,即可得到结论.
| OM |
| 1 |
| 2 |
| a |
| b |
| OG |
| 1 |
| 3 |
| a |
| b |
| PG |
| GQ |
解答:证明:∵
=
,
=
,M是AB边的中点
∴
=
(
+
)
∵点G是△ABO的重心,∴
=
(
+
)
∵PQ过△ABO的重心G,∴
=λ
∴
(
+
)-m
=n
-
(
+
)
∵
,
不共线
∴
消去λ,可得3mn=m+n
∴
+
=3.
| OA |
| a |
| OB |
| b |
∴
| OM |
| 1 |
| 2 |
| a |
| b |
∵点G是△ABO的重心,∴
| OG |
| 1 |
| 3 |
| a |
| b |
∵PQ过△ABO的重心G,∴
| PG |
| GQ |
∴
| 1 |
| 3 |
| a |
| b |
| a |
| b |
| 1 |
| 3 |
| a |
| b |
∵
| a |
| b |
∴
|
消去λ,可得3mn=m+n
∴
| 1 |
| m |
| 1 |
| n |
点评:本题考查向量知识的运用,考查平面向量基本定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
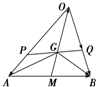 如图所示,已知点G是△ABO的重心.
如图所示,已知点G是△ABO的重心.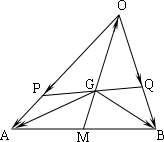
 =a,
=a, =b,
=b, =ma,
=ma,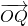 =nb,求证:
=nb,求证: +
+ =3.
=3.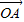 =
=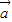 ,
,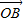 =
=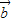 ,
,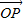 =m
=m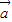 ,
,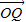 =n
=n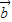 ,求证:
,求证: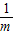 +
+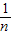 =3.
=3.