题目内容
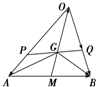 如图所示,已知点G是△ABO的重心.
如图所示,已知点G是△ABO的重心.(1)求
| GA |
| GB |
| GO |
(2)若PQ过△ABO的重心G,且
| OA |
| a |
| OB |
| b |
| OP |
| a |
| OQ |
| b |
| 1 |
| m |
| 1 |
| n |
分析:(1)利用向量的线性运算,结合点G是△ABO的重心,即可得到结论;
(2)由于P,G,Q三点共线,利用向量共线定理,可得存在实数λ使得
=λ
,利用平面向量基本定理,可得方程组,消去λ,即可得到结论.
(2)由于P,G,Q三点共线,利用向量共线定理,可得存在实数λ使得
| PG |
| GQ |
解答:(1)解:∵M为AB中点,∴
=
(
+
).
又G为△ABO的重心,∴
=
,
∴
+
+
=2
-2
=
.
(2)证明:由
=
(a+b)得,
=
=
(a+b).
由于P,G,Q三点共线,∴存在实数λ使得
=λ
.
而
=
-
=(
-m)a+
b,
=
-
=-
a+(n-
)b,
则(
-m)a+
b=λ[-
a+(n-
)b],
∴
,消去λ整理得
+
=3.
| GM |
| 1 |
| 2 |
| GA |
| GB |
又G为△ABO的重心,∴
| GM |
| 1 |
| 2 |
| OG |
∴
| GA |
| GB |
| GO |
| GM |
| GM |
| 0 |
(2)证明:由
| OM |
| 1 |
| 2 |
| OG |
| 2 |
| 3 |
| OM |
| 1 |
| 3 |
由于P,G,Q三点共线,∴存在实数λ使得
| PG |
| GQ |
而
| PG |
| OG |
| OP |
| 1 |
| 3 |
| 1 |
| 3 |
| GQ |
| OQ |
| OG |
| 1 |
| 3 |
| 1 |
| 3 |
则(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴
|
| 1 |
| m |
| 1 |
| n |
点评:本题考查向量知识的运用,考查向量共线定理、考查平面向量基本定理,属于中档题.

练习册系列答案
相关题目
 如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足
如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足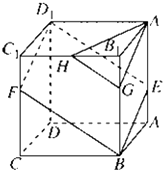 如图所示,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.
如图所示,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.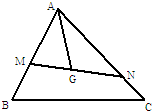 如图所示,已知点G是△ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且
如图所示,已知点G是△ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且 ,则
,则 的值为
.
的值为
.