Question

设f(x)=ax²＋bx，且－1≤f(－1)≤2，2≤f(1)≤4，求f(－2)的取值范围.

Answer 1

解:∵f(－1)=a－b，－1≤f(－1)≤2,∴－1≤a－b≤2.

∵f(1)=a＋b，2≤f(1)≤4，∴2≤a＋b≤4.

∴a、b满足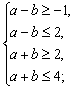

f(－2)=4a－2b.在直角坐标系aOb中作出上面的不等式组所表示的平面区域(如图),即可行域(四边形ABCD的边界或其内部).

作直线l:4a－2b=0，即直线l:2a－b=0，

把直线平移至l₁的位置时，直线经过可行域上的点B，且与原点的距离最大；把直线l平移至l₂的位置时，直线经过可行域上的点D，且与原点的距离最小.

由得B点的坐标为(3，1)；

由得D点的坐标为(，).

∴f(－2)的最大值为f(－2)=4a－2b=4×3－2×1＝10.

f(－2)的最小值为f(－2)=4×－2×＝－1.

∴－1≤f(－2)≤10为所求.