题目内容
17.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点F是抛物线y2=8x焦点,两曲线的一个公共点为P,且|PF|=5,则该双曲线的离心率为( )| A. | 2 | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 根据抛物线和双曲线有相同的焦点求得c=2,根据抛物线的定义可以求出P的坐标,运用双曲线的定义求得2a=2,然后求得离心率e.
解答 解:抛物线y2=8x焦点F(2,0),准线方程为x=-2,
设P(m,n),
由抛物线的定义可得|PF|=m+2=5,
解得m=3,
则n2=24,即有P(3,±2$\sqrt{6}$),
可得左焦点F'为(-2,0),
由双曲线的定义可得2a=|PF'|-|PF|=$\sqrt{25+24}$-$\sqrt{1+24}$=7-5=2,即a=1,
即有e=$\frac{c}{a}$=2.
故选A.
点评 本题主要考查了双曲线,抛物线的定义和简单性质,主要考查了离心率的求法,解答关键是利用抛物线和双曲线的定义.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
7.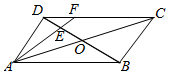 在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )
在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )
 在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )
在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | 1 |
8.若复数z满足(-3+4i)$\overline{z}$=25i,其中i为虚数单位,则z=( )
| A. | 4-3i | B. | 4+3i | C. | -5+3i | D. | 3+4i |
5.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)单调递减,若实数a满足f(log3a)+f(${log}_{\frac{1}{3}}$a)≤2f(2),则a的取值范围是( )
| A. | [$\frac{1}{9}$,9] | B. | (-∞,$\frac{1}{9}$] | C. | [$\frac{1}{2}$,2] | D. | (0,$\frac{1}{9}$]∪[9,+∞] |
12.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量,成本和售价如下表:
分别用x,y表示黄瓜和韭菜的种植面积(单位:亩)
(Ⅰ)用x,y列出满足条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别种植黄瓜和韭菜各对少亩能够使一年的种植总利润(总利润=总销售收入-总种植成本)最大?并求出此最大利润.
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
(Ⅰ)用x,y列出满足条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别种植黄瓜和韭菜各对少亩能够使一年的种植总利润(总利润=总销售收入-总种植成本)最大?并求出此最大利润.
2.设集合A={x|y=lg(x-3)},B={y|y=2x,x∈R},则A∪B等于( )
| A. | ∅ | B. | R | C. | {x|x>1} | D. | {x|x>0} |
13.下列各组函数中,表示同一函数的是( )
| A. | f(x)=2log2x,$g(x)={log_2}{x^2}$ | B. | f(x)=|x|,$g(x)={(\sqrt{x})^2}$ | ||
| C. | f(x)=x,$g(x)=lo{g_2}{2^x}$ | D. | f(x)=x+1,$g(x)=\frac{x^2}{x}-1$ |
14.已知函数y=f(x+1)的图象关于直线x=-1对称,且满足f(x)+f′(x)=2ex,若a=f(-3),b=f(lnπ),c=f(|sinx|),则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |