题目内容
曲线C:y=2x3-3x2-2x+1,点P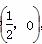 ,求过P的切线l与C围成的图形的面积.
,求过P的切线l与C围成的图形的面积.
解析 设切点坐标为(x0,y0)
y′=6x2-6x-2,
则y′|x=x0=6x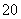 -6x0-2,
-6x0-2,
切线方程为y=(6x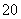 -6x0-2)
-6x0-2) ,
,
则y0=(6x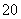 -6x0-2)
-6x0-2)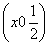 ,
,
即2x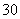 -3x
-3x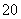 -2x0+1=(6x
-2x0+1=(6x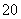 -6x0-2)
-6x0-2)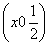 .
.
整理得x0(4x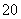 -6x0+3)=0,
-6x0+3)=0,
解得x0=0,则切线方程为y=-2x+1.
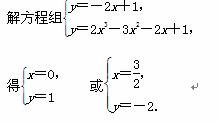 由y=2x3-3x2-2x+1与y=-2x+1的图象可知
由y=2x3-3x2-2x+1与y=-2x+1的图象可知

练习册系列答案
相关题目
 m B.
m B.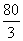 m C.
m C.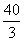 m D.
m D.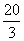 m
m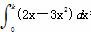 =0,则k等于_________.
=0,则k等于_________.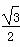 ,且角α的终边经过点(x,2),则P点的横坐标x是( ).
,且角α的终边经过点(x,2),则P点的横坐标x是( ).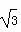 B.±2
B.±2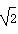 D.-2
D.-2 +cos α,且α∈
+cos α,且α∈ ,则
,则 的值为________.
的值为________. ,-
,- =
= ,cos
,cos =
= ,则cos
,则cos =( ).
=( ). D.-
D.-