题目内容
 (1)如图,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,证明两角差的余弦公式:cos(α-β)=cosαcosβ+sinαsinβ;
(1)如图,已知α、β是坐标平面内的任意两个角,且0≤α-β≤π,证明两角差的余弦公式:cos(α-β)=cosαcosβ+sinαsinβ;(2)已知α∈(0,
| π |
| 2 |
| π |
| 2 |
| 1 |
| 3 |
| 7 |
| 9 |
分析:(1)设P1、P2分别为α、β终边与单位圆的交点,表示出P1、P2坐标,利用平面向量的数量积运算法则根据两点坐标表示出
•
,再由
•
的夹角为α-β,两向量模为1,利用平面向量数量积运算法则表示出
•
,即可得证;
(2)由β的范围求出sinβ大于0,根据cosβ的值,利用同角三角函数间的基本关系求出sinβ的值,由α与β的范围求出α+β的范围,根据sin(α+β)的值,利用同角三角函数间的基本关系求出cos(α+β)的值,由cosα=cos[(α+β)-β],利用两角和与差的余弦函数公式化简后,将各自的值代入计算求出cosα的值,所求式子第一项利用二倍角的余弦函数公式化简后,去括号合并将cosα的值代入计算即可求出值.
| OP1 |
| OP2 |
| OP1 |
| OP2 |
| OP1 |
| OP2 |
(2)由β的范围求出sinβ大于0,根据cosβ的值,利用同角三角函数间的基本关系求出sinβ的值,由α与β的范围求出α+β的范围,根据sin(α+β)的值,利用同角三角函数间的基本关系求出cos(α+β)的值,由cosα=cos[(α+β)-β],利用两角和与差的余弦函数公式化简后,将各自的值代入计算求出cosα的值,所求式子第一项利用二倍角的余弦函数公式化简后,去括号合并将cosα的值代入计算即可求出值.
解答:(1)证明:设P1、P2分别为α、β终边与单位圆的交点,
∴P1(cosα,sinα),P2(cosβ,sinβ),
∴
•
=cosαcosβ+sinαsinβ,
又∵
•
的夹角为α-β,
∴
•
=|OP1|•|OP2|cos(α-β)=cos(α-β),
∴cos(α-β)=cosαcosβ+sinαsinβ;
(2)∵β∈(
,π),cosβ=-
,
∴sinβ=
=
,
∵α∈(0,
),∴α+β∈(
,
),
∵sin(α+β)=
,
∴cos(α+β)=-
=-
,
∴cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ=
,
则2cos2α+cos2α=2(2-cos2α1)+cos2α=5cos2α-2=
.
∴P1(cosα,sinα),P2(cosβ,sinβ),
∴
| OP1 |
| OP2 |
又∵
| OP1 |
| OP2 |
∴
| OP1 |
| OP2 |
∴cos(α-β)=cosαcosβ+sinαsinβ;
(2)∵β∈(
| π |
| 2 |
| 1 |
| 3 |
∴sinβ=
| 1-cos2β |
2
| ||
| 3 |
∵α∈(0,
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
∵sin(α+β)=
| 7 |
| 9 |
∴cos(α+β)=-
| 1-sin2(α+β) |
4
| ||
| 9 |
∴cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ=
2
| ||
| 3 |
则2cos2α+cos2α=2(2-cos2α1)+cos2α=5cos2α-2=
| 22 |
| 9 |
点评:此题考查了两角和与差的余弦函数公式,二倍角的余弦函数公式,同角三角函数间的基本关系,以及平面向量的数量积运算,熟练掌握公式是解本题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目

 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
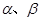 是坐标平面内的任意两个角,且
是坐标平面内的任意两个角,且 ,证明两角差的余弦公式:
,证明两角差的余弦公式: ;
; ,且
,且 ,
, ,求
,求 的值.
的值.