题目内容

如果（x2-
2
x3
）n的展开式中含有非零常数项，则正整数n的最小值为（　　）
A、3B、5C、6D、10
考点：二项式定理的应用
专题：二项式定理
分析：先求出二项式展开式的通项公式，再令x的幂指数等于0，求得n与r的关系，可得n的最小值．
解答： 解：由于（x2-
2
x3
）n的展开式的通项公式为 Tr+1=
C
r
n
•（-2）r•x2n-5r，
令2n-5r=0，求得n=
5r
2
，由r为自然数，可得n的最小值为5，此时r=2，
故选：B．
点评：本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于基础题．
练习册系列答案
相关题目
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，右焦点为F（1，0）．
（1）求此椭圆的标准方程．
（2）若过点F且倾斜角为
3π
4
的直线与此椭圆交于A、B两点，求|AB|的值．
已知函数f（x）=logax+3过点（4，5），则方程f（x）-f′（x）=2的解所在的区间是
 
．
如图：底面是矩形ABCD，PA⊥底面ABCD，则图中直角三角形的个数（　　）
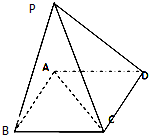
A、8B、7C、6D、5
已知定义在R上的奇函数f（x）满足：当x＞0时，f（x）=|x-a2|-a2，若对任意的x∈R，恒有f（x+a）≥f（x），则实数a的取值范围为
 
．
奇函数f（x）的定义域为R，当x≥0时，f（x）=2x-x2，设函数y=f（x），x∈[a，b]的值域为[
1
a
，
1
b
]（a≠b），求a，b的值．
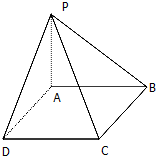如图，四棱锥P-ABCD的底面是边长为1的正方形，PA⊥CD，PA=1，PD=
2
．
（1）求证：PA⊥平面ABCD；
（2）求四棱锥P-ABCD的体积；
（3）求四棱锥P-ABCD的表面积．
已知{an}是各项为正数的等差数列，a1，a2，a4成等比数列．令bn=
1
a2n
，n=1，2，3…．
（1）证明{bn}为等比数列；
（2）如果无穷数列{bn}各项的和S=
1
3
，求数列{an}的首项a1和公差d；
（3）在（2）的条件下令cn=an+1，是否存在m，k∈N，有cm+cm+1=ck？说明理由．
已知双曲线
x2
10-m
+
y2
m-2
=1的实轴在y轴上且焦距为8，则双曲线的渐近线方程为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网