题目内容
光线沿直线y=2x+1的方向射在直线y=x上.求反射后的光线所在的直线方程.
思路解析：根据光学知识，入射角等于反射角，可以根据夹角公式求解，也可以利用对称来求解,后一种更方便. 解法一：设P（x，y）是反射后的光线所在直线上任意一点，由光学知识可知P关于y=x的对称点P′（x0，y0）在直线y=2x+1上，∴y0=2x0+1. 而 事实上，只需将y=2x+1中的x，y对调，便可得出此曲线关于直线y=x的对称曲线的方程. 解法二：解方程组 在直线y=2x+1上任取一点A（1，3），A点关于直线y=x的对称点B（3，1）必在反射光线所在的直线上， ∴反射光线的方程为PB： 解法三：由方程组 由光学知识可知入射线与反射线关于直线x+y+2=0对称. 在y=2x+1上任取一点C（0，1），关于直线x+y+2=0的对称点为D（-3，-2）. 直线PD： 解法四：解方程组 设直线y=x到y=2x+1的角为α，则tanα= 设反射光线所在直线的斜率为k,则 解法五：在y=2x+1上任取两点A（0，1）、B（-1，-1），它们关于y=x的对称点为A′（1，0）、B′（-1，-1）.A′B′所在的直线方程为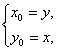
所以反射光线所在的直线方程为x=2y+1，即x-2y-1=0.
得交点P（-1，-1）.
=
，即x-2y-1=0.
得交点P（-1，-1）.过P点且垂直直线y=x的直线方程为x+y+2=0.
=
，即x-2y-1=0为反射光线所在直线的方程.
得交点P（-1，-1）.
=
.
=
，则k=
，则反射光线所在直线的方程为y+1=
（x+1），即x-2y-1=0.
=
，即x-2y-1=0为反射光线所在的直线方程.
假期学苑四川教育出版社系列答案
期末复习加暑假作业延边教育出版社系列答案
乐享假期暑假作业延边教育出版社系列答案
仁爱英语开心暑假科学普及出版社系列答案
仁爱英语同步听力训练系列答案
仁爱英语同步学案系列答案
仁爱英语同步整合方案系列答案
仁爱英语同步活页AB卷系列答案
仁爱英语同步练习与测试系列答案
仁爱英语同步练习簿系列答案
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
x-1 B.y=
x-
x+
D.y=
x+1