题目内容
求函数f(x)=x3+x2-2x-2的一个为正数的零点(精确到0.1).
解析:一般地,对于高次多项式函数及其他的一些函数,不适宜作具体计算,有必要寻求其零点的近似解的方法.
解:函数f(x)=x3+x2-2x-2的图象如下图,由于f(0)=-2<0,f(2)>0,可取区间[0,2]作为计算的初始区间.
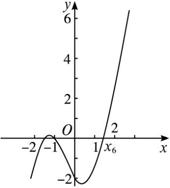
用二分法逐次计算,列表如下:
端点(中点)坐标 | 计算中点的函数值 | 取区间 |
f(0)=-2<0 | f(2)=6>0 | [0,2] |
x1=(0+2)/2=1 | f(x1)=-2<0 | [1,2] |
x2=(1+2)/2=1.5 | f(x2)=0.625>0 | [1,1.5] |
x3=(1+1.5)/2=1.25 | f(x3)=-0.984<0 | [1.25,1.5] |
x4=(1.25+1.5)/2=1.375 | f(x4)=-0.26<0 | [1.375,1.5] |
x5=(1.375+1.5)/2=1.438 | f(x5)=0.165>0 | [1.375,1.438] |
x6=(1.375+1.438)/2=1.406 5 | f(x6)=0.028 9>0 |
|
由上表的计算可知,区间[1.375,1.438]的长度小于0.1,所以这个区间的中点x6≈1.406 5可作为所求函数的一个正实数零点的近似值.

练习册系列答案
相关题目