题目内容
已知f(x)=-2asin(2x+
)+2a+b,
(1)求f(x)的周期
(2)若a>0,求f(x)的最大值,并求出取得最大值时的x的集合.
(3)若x∈[
,
],是否存在常数a、b∈Q,使得f(x)的值域为{y|-3≤y≤
-1}?若存在,求出a、b的值;若不存在,说明理由.
| π |
| 6 |
(1)求f(x)的周期
(2)若a>0,求f(x)的最大值,并求出取得最大值时的x的集合.
(3)若x∈[
| π |
| 4 |
| 3π |
| 4 |
| 3 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值
分析:(1)根据函数y=Asin(ωx+φ)的周期为
,求得结果.
(2)由条件根据正弦函数的定义域和值域,求得f(x)的最大值以及取得最大值时的x的集合.
(3)由x∈[
,
],可得sin( 2x+
)∈[-1,
].分①当a>0时、②当a<0时两种情况分别求得a、b的值,从而得出结论.
| 2π |
| ω |
(2)由条件根据正弦函数的定义域和值域,求得f(x)的最大值以及取得最大值时的x的集合.
(3)由x∈[
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
| ||
| 2 |
解答:
解:(1)∵f(x)=-2asin(2x+
)+2a+b,∴T=π.
(2)∵a>0,∴f(x)max=-2a×(-1)+2a+b=4a+b.
由2x+
=2kπ-
,k∈Z,解得x=kπ-
,k∈Z,
∴取得最大值时的x的集合为:{x|x=kπ-
,k∈Z}.
(3)存在a=-1,b=1,满足条件.
∵x∈[
,
],∴2x+
∈[
,
],
∴sin( 2x+
)∈[-1,
].
若存在这样的有理数a、b,则
①当a>0时,
,这不可能;
②当a<0时,
,解得a=-1,b=1,
故存在a=-1,b=1,满足条件.
| π |
| 6 |
(2)∵a>0,∴f(x)max=-2a×(-1)+2a+b=4a+b.
由2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∴取得最大值时的x的集合为:{x|x=kπ-
| π |
| 3 |
(3)存在a=-1,b=1,满足条件.
∵x∈[
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
| 2π |
| 3 |
| 5π |
| 3 |
∴sin( 2x+
| π |
| 6 |
| ||
| 2 |
若存在这样的有理数a、b,则
①当a>0时,
|
②当a<0时,
|
故存在a=-1,b=1,满足条件.
点评:本题主要考查三角恒等变换,正弦函数的周期性、最值、定义域和值域,属于中档题.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为x-2y=0,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
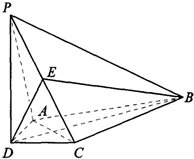 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E是PC的中点,AD=CD=1,
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E是PC的中点,AD=CD=1,