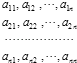��Ŀ����
����Ŀ�����������������ҹ��Ŵ���ѧ���������ڼ���ѧ�е��о���������1ǧ���꣮�ڡ������������У�������Ϊֱ�������Σ��Ҳ��ⴹֱ�ڵ������������Ϊǵ�£�����ָ����Ϊ���Σ�һ���ⴹֱ�ڵ������������Ğָ�ĸ����Ϊֱ�������ε������壮��ͼ����ǵ��ABC��A1B1C1�У�AC��BC�� 
������֤������B��A1ACC1Ϊ���������ж�������B��A1CC1�Ƿ�Ϊ��Ğ�����ǣ���д���������ֱ�ǣ�ֻҪ��д�����ۣ���
������A1A=AB=2��������B��A1ACC1������ʱ��������C��A1B��C1������ֵ��
���𰸡�֤����������ǵ��ABC��A1B1C1�����ʵã��ı���A1ACC1�Ǿ��Σ� ��A1A�͵���ABC��BCƽ��ABC��
��BC��A1A����BC��AC��A1A��AC=A��A1A��ACƽ��A1ACC1 ��
��BC��ƽ��A1ACC1 ��
������B��A1ACC1������
������B��A1CC1�Ƿ�Ϊ��Ğ���ĸ����ֱ�Ƿֱ��ǡ�A1CB����A1C1C����BCC1 �� ��A1C1B��
�⣺����A1A=AB=2��
�ɣ���֪����B��A1ACC1�������![]() =
= ![]() =
= ![]() ��
�� ![]() ��
��
���ҽ���AC=BC= ![]() ʱ��
ʱ�� ![]() ��
��
��CΪԭ�㣬CBΪx�ᣬCAΪy�ᣬCC1Ϊz�ᣬ�����ռ�ֱ������ϵ��
��A1��0�� ![]() ��2����B��
��2����B�� ![]() ��0��0����C1��0��0��2����
��0��0����C1��0��0��2����
�� ![]() =��0��
=��0�� ![]() ��2����
��2���� ![]() =��
=�� ![]() ��0��0����
��0��0���� ![]() =��0��
=��0�� ![]() ��0����
��0���� ![]() =��
=�� ![]() ��0����2����
��0����2����
��ƽ��CA1B�ķ����� ![]() =��x��y��z����
=��x��y��z����
��  ��ȡy=
��ȡy= ![]() ����
���� ![]() =��0��
=��0�� ![]() ����1����
����1����
��ƽ��C1A1B�ķ����� ![]() =��a��b��c����
=��a��b��c����
��  ��ȡa=
��ȡa= ![]() ����
���� ![]() =��
=�� ![]() ��0��1����
��0��1����
�赱����B��A1ACC1������ʱ�������C��A1B��C1��ƽ���Ϊ�ȣ�
��cos��= ![]() =
= ![]() =
= ![]() ��
��
�൱����B��A1ACC1������ʱ�������C��A1B��C1������ֵΪ ![]()
��������������ǵ��ABC��A1B1C1�����ʵã��ı���A1ACC1�Ǿ��Σ��Ƶ���BC��A1A��BC��AC���Ӷ�BC��ƽ��A1ACC1 �� �ɴ���֤������B��A1ACC1Ϊ������������B��A1CC1�Ƿ�Ϊ��Ğ���ĸ����ֱ�Ƿֱ��ǡ�A1CB����A1C1C����BCC1 �� ��A1C1B����������B��A1ACC1������� ![]() ��
�� ![]() �����ҽ���AC=BC=
�����ҽ���AC=BC= ![]() ʱ��
ʱ�� ![]() ����CΪԭ�㣬CBΪx�ᣬCAΪy�ᣬCC1Ϊz�ᣬ�����ռ�ֱ������ϵ�����������������������B��A1ACC1������ʱ�������C��A1B��C1������ֵ��
����CΪԭ�㣬CBΪx�ᣬCAΪy�ᣬCC1Ϊz�ᣬ�����ռ�ֱ������ϵ�����������������������B��A1ACC1������ʱ�������C��A1B��C1������ֵ��
�����㾫����ͨ������������Ľṹ������ֱ����ƽ�洹ֱ�����ʣ����ղ��桢�Խ��涼�������Σ�ƽ���ڵ���Ľ�����������ƣ������Ʊȵ��ڶ��㵽���������ߵıȵ�ƽ������ֱ��ͬһ��ƽ�������ֱ��ƽ�м����Խ����⣮