Question

【题目】点在圆上运动，轴，为垂足，点在线段上，满足．

（1）求点的轨迹方程；

（2）过点作直线与点的轨迹相交于两点，使点为弦的中点，求直线的方程．

Answer 1

【答案】（1） ;（2）.

【解析】

试题分析：（1）由条件可知，点是的中点，所以根据求什么设什么的原则，设点，则，代入方程，可求得点的轨迹方程；（2）此题为直线与椭圆相交的中点弦问题，设直线方程为，与椭圆方程联立，根据韦达定理可得根与系数的关系，利用点是两点的中点，可求得直线的斜率，即得直线方程.

试题解析：（1）∵点在线段上，满足，∴点是线段的中点，

设，则，

∵点在圆上运动，则，即，

∴点的轨迹方程为．

（2）当直线轴时，由椭圆的对称性可得弦的中点在轴上，不可能是点，这种情况不满足题意．

设直线的方程为，

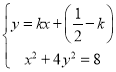由可得，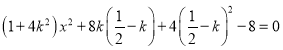

由韦达定理可得，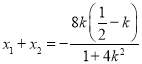

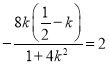由的中点为，可得，解得，

即直线的方程为，∴直线的方程为．