题目内容
【题目】设![]() ,函数
,函数![]() (
(![]() 是自然对数的底数).
是自然对数的底数).
(1)证明:存在一条定直线![]() 与曲线
与曲线![]() 和
和![]() 都相切;
都相切;
(2)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的值
的值
【答案】(1)证明见解析;(2)![]()
【解析】
试题分析:(1)此题证明关键是找出一条公切线,先求导数,![]() ,
,![]() ,
,![]() ,正巧
,正巧![]() ,即这两个函数图象有公共点
,即这两个函数图象有公共点![]() ,且此点处两函数的导数相等,这点处的切线就是公切线;(2)若
,且此点处两函数的导数相等,这点处的切线就是公切线;(2)若![]() 对
对![]() 恒成立,即
恒成立,即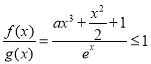 ,记
,记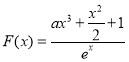 ,由于
,由于![]() ,因此
,因此![]() 是
是![]() 的最大值,又
的最大值,又![]() ,在
,在![]() 附近
附近![]() ,记
,记![]() ,因此必有
,因此必有![]() ,从而得
,从而得![]() ,接着检验
,接着检验![]() 时,
时,![]() 最大值.
最大值.
试题解析:(1)证明:函数![]() 的导数分别为
的导数分别为![]() ,
,
注意到对任意![]() ,
,
故直线![]() 与曲线
与曲线![]() 与
与![]() 都相切
都相切
(2)设函数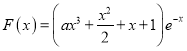 ,则对任意
,则对任意![]() ,都有
,都有![]() .
.
因对任意![]() ,都有
,都有![]() ,故
,故![]() 为
为![]() 的极大值点
的极大值点
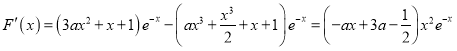 ,
,
记![]() ,则
,则![]() ,
,
注意到在![]() 的附近,恒有
的附近,恒有![]() ,
,
故要使![]() 为
为![]() 的极大值点,
的极大值点,
必须![]() (否则,若
(否则,若![]() ,则在
,则在![]() 的附近,恒有
的附近,恒有![]() ,从而
,从而![]() ,于是
,于是![]() 不是
不是![]() 的极值点;同理,若
的极值点;同理,若![]() ,则
,则![]() 也不是
也不是![]() 的极值点),即
的极值点),即![]() ,从而
,从而![]()
又当![]() 时,
时,![]() ,
,
则在![]() 上,
上,![]() ,在
,在![]() 上,
上,![]() ,
,
于是![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
故![]() .
.
综上所述,![]()

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
