题目内容
20.下面的各图中,散点图与相关系数r不符合的是( )| A. | 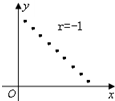 | B. | 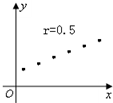 | C. | 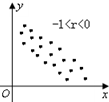 | D. | 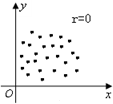 |
分析 根据|r|的值越接近于1时,两个变量的相关关系越明显,|r|越接近于0时,两个变量的相关关系越不明显,结合题意即可做出正确的选择.
解答 解:对于A,变量x,y的散点图是一条斜率小于0的直线,所以相关系数r=-1,所以A正确;
对于B,变量x,y的散点图是一条斜率大于0的直线,所以相关系数r=1,所以B错误;
对于C,变量x,y的散点图从左到右是向下的带状分布,所以相关系数-1<r<0,所以C正确;
对于D,变量x,y的散点图中,x、y之间的样本相关关系非常不明显,所以相关系数r最接近0,D正确.
故选:B.
点评 本题考查了两个变量线性相关关系的判断问题,是基础题目.

练习册系列答案
相关题目
8.如果a<b<0,那么下面一定成立的是( )
| A. | ac<bc | B. | a-b>0 | C. | a2>b2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
15.设α、β、γ是三个不同的平面,a、b是两条不同的直线,下列四个命题中正确的是( )
| A. | 若a∥α,b∥α,则a∥b | |
| B. | 若a⊥α,b⊥β,a⊥b,则α⊥β | |
| C. | 若a∥α,b∥β,a∥b,则α∥β | |
| D. | 若a,b在平面α内的射影互相垂直,则a⊥b |
5.已知数列{an}满足a1=1,an-an-1=n(n≥2),则数列{an}的通项公式an=( )
| A. | $\frac{1}{2}n(n+1)$ | B. | $\frac{1}{2}n(3n-1)$ | C. | n2-n+1 | D. | n2-2n+2 |
12.已知三棱柱ABC-A1B1C1,所有棱长为都为2,顶点B1在底面ABC内的射影是△ABC的中心,则四面体A1-ABC,B1-ABC,C1-ABC公共部分的体积为( )
| A. | $\frac{2\sqrt{2}}{9}$ | B. | $\frac{2\sqrt{3}}{9}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
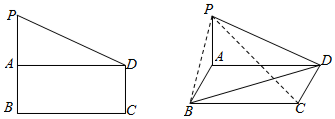 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ:
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ: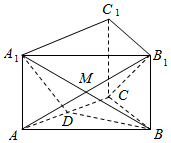 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,△ABC是边长为2的正三角形,D是AC的中点.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,△ABC是边长为2的正三角形,D是AC的中点.