题目内容
10.设棱长为a的正方体的体积和表面积分别为V1,S1,底面半径高均为r的圆锥的体积和侧面积分别为V2,S2,若$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{π}$,则$\frac{{S}_{1}}{{S}_{2}}$的值为$\frac{3\sqrt{2}}{π}$.分析 根据体积比得出a和r的关系,代入面积公式求出面积比即可.
解答 解:圆锥的母线l=$\sqrt{{r}^{2}+{r}^{2}}$=$\sqrt{2}$r.
V1=a3,S1=6a2,V2=$\frac{1}{3}π{r}^{3}$,S2=πrl=$\sqrt{2}$πr2.
∵$\frac{{V}_{1}}{{V}_{2}}$=$\frac{{a}^{3}}{\frac{1}{3}π{r}^{3}}$=$\frac{3}{π}$,∴a=r.
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{6{a}^{2}}{\sqrt{2}π{r}^{2}}$=$\frac{3\sqrt{2}}{π}$.
故答案为:$\frac{3\sqrt{2}}{π}$.
点评 本题考查了圆锥,正方体的体积和表面积计算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下面的各图中,散点图与相关系数r不符合的是( )
| A. | 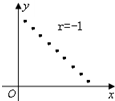 | B. | 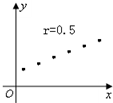 | C. | 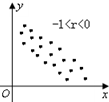 | D. | 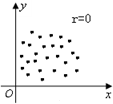 |
1.已知i为虚数单位,(1+i)(2-i)=a+bi,其中a,b∈R,则( )
| A. | a=1,b=1 | B. | a=3,b=1 | C. | a=1,b=0 | D. | a=3,b=0 |
2.下列说法错误的是( )
| A. | 数列4,7,3,4的首项是4 | |
| B. | 数列{an}中,若a1=3,则从第2项起,各项均不等于3 | |
| C. | 数列-1,0,1,2与数列0,1,2,-1不相同 | |
| D. | 数列中的项不能是三角形 |
19.已知8>7,16>9,32>11,…,则有( )
| A. | 2n>2n+1 | B. | 2n+1>2n+1 | C. | 2n+2>2n+5 | D. | 2n+3>2n+7 |