题目内容
若双曲线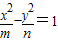
（mn≠0）的一个焦点与抛物线y2=4x的焦点重合，且离心率为2，则mn的值为（ ）A．
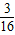
B．
C．
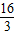
D．
【答案】分析：依题意，可求得双曲线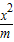
-
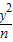=1的右焦点F′（1，0），从而有m+n=1，再结合其离心率为2可求得mn的值．
解答：解：∵抛物线y2=4x的焦点为（1，0），
∴由题意得，双曲线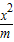
-
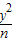=1的右焦点F′（1，0），且m＞0，n＞0，
∴m+n=1，①
又双曲线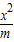
-
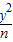=1的离心率为2，
∴
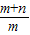=4②
由①②解得：m=
，n=
，
∴mn=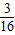
．
故选A．
点评：本题考查双曲线与抛物线的简单性质，考查方程思想与运算能力，属于中档题．
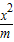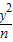-=1的右焦点F′（1，0），从而有m+n=1，再结合其离心率为2可求得mn的值．解答：解：∵抛物线y2=4x的焦点为（1，0），
∴由题意得，双曲线
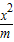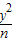-=1的右焦点F′（1，0），且m＞0，n＞0，∴m+n=1，①
又双曲线
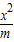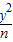-=1的离心率为2，∴
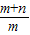=4②由①②解得：m=
，n=，∴mn=
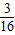．故选A．
点评：本题考查双曲线与抛物线的简单性质，考查方程思想与运算能力，属于中档题．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
（2007•南京二模）已知F为椭圆