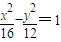题目内容
若双曲线mx2-ny2=1(mn≠0)离心率为
,且有一个焦点与抛物线y2=2x的焦点重合,则m=
| 2 |
8
8
.分析:先确定抛物线的焦点坐标,双曲线的标准方程,利用双曲线mx2-ny2=1(mn≠0)离心率为
,且有一个焦点与抛物线y2=2x的焦点重合,可得两方程,从而可求m的值.
| 2 |
解答:解:由题意,抛物线y2=2x的焦点坐标为(
,0),双曲线mx2-ny2=1可化为:
-
=1
∴a2=
,b2=
,c2=a2+b2=
+
∵双曲线mx2-ny2=1(mn≠0)离心率为
,
∴
=2
∴m=n
∵双曲线mx2-ny2=1(mn≠0)有一个焦点与抛物线y2=2x的焦点重合
∴
+
=
∴m=8
故答案为:8
| 1 |
| 2 |
| x2 | ||
|
| y2 | ||
|
∴a2=
| 1 |
| m |
| 1 |
| n |
| 1 |
| m |
| 1 |
| n |
∵双曲线mx2-ny2=1(mn≠0)离心率为
| 2 |
∴
| ||||
|
∴m=n
∵双曲线mx2-ny2=1(mn≠0)有一个焦点与抛物线y2=2x的焦点重合
∴
| 1 |
| m |
| 1 |
| n |
| 1 |
| 4 |
∴m=8
故答案为:8
点评:本题以抛物线为载体,考查双曲线的标准方程,解题的关键是正确运用抛物线、双曲线的几何性质,计算要小心.

练习册系列答案
相关题目
 的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( ) =1
=1 =1
=1
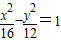
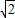 ,且有一个焦点与抛物线y2=2x的焦点重合,则m= .
,且有一个焦点与抛物线y2=2x的焦点重合,则m= . 的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( ) =1
=1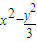 =1
=1