题目内容
1.函数y=cosx•ln$\frac{{x}^{2}+2}{{2(x}^{2}+1)}$,x∈[-$\frac{π}{2}$,$\frac{π}{2}$]的图象大致为( )| A. |  | B. | 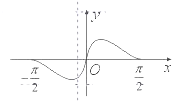 | ||
| C. | 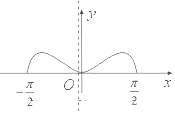 | D. | 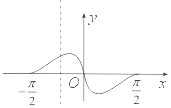 |
分析 利用函数的奇偶性排除选项,利用函数的特殊值对应点的位置排除选项得到结果.
解答 解:函数y=cosx•ln$\frac{{x}^{2}+2}{{2(x}^{2}+1)}$,x∈[-$\frac{π}{2}$,$\frac{π}{2}$]是偶函数,排除B,D,
当x=$\frac{π}{4}$时,y=$\frac{\sqrt{2}}{2}$•ln$\frac{\frac{{π}^{2}+8}{4}}{2(\frac{{π}^{2}+4}{4})}$=$\frac{\sqrt{2}}{2}$ln$\frac{{π}^{2}+8}{2{π}^{2}+8}$<0,排除C,
故选:A.
点评 本题考查函数的图象的判断,函数的奇偶性以及特殊值的判断是常用方法,考查计算能力.

练习册系列答案
相关题目
13.已知实数a,b,c满足不等式0<a<b<c<1,且M=2a,N=3-b,P=lnc,则M,N,P的大小关系是( )
| A. | P<N<M | B. | P<M<N | C. | M<P<N | D. | N<P<M |
10.已知$\overrightarrow{a}$=(1,sin2x),$\overrightarrow{b}$=(2,sin2x),其中x∈(0,π),若|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|,则tanx的值等于( )
| A. | -1 | B. | 1 | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
11.设函数f(x)=$\left\{\begin{array}{l}{2x+4,x≤0}\\{{2}^{x},x>0}\end{array}\right.$,若f[f(a)]>f[f(a)+1],则实数a的取值范围为( )
| A. | $(-\frac{5}{2},-2]$ | B. | $[-\frac{5}{2},-2]$ | C. | [-2,0) | D. | [-2,0] |
