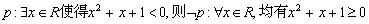题目内容
已知函数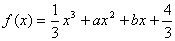 (
( 是实数),且
是实数),且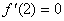 ,
,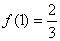 ,
,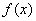 在闭区间
在闭区间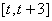 上的最小值为
上的最小值为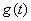 (
(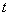 为实数),
为实数),
(Ⅰ)求实数 的值; (Ⅱ)当
的值; (Ⅱ)当 时,求
时,求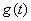 的取值范围.
的取值范围.
解:(Ⅰ) ,由
,由 --
--
得 ,
,
(Ⅱ) ,
,
因为 =
= ,所以
,所以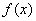 在
在 递增,
递增, 递减,
递减, 递增。
递增。
可知 ,所以
,所以 ,即有
,即有 ,结合图形,
,结合图形,
(1)当 ,即
,即 时,
时, =
= -
-
 (2)当
(2)当 ,且
,且 ,即
,即 时,
时,
(3)当 时,
时, =
= -
-
综上,
若 ,则
,则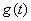 在
在 恒等于
恒等于 ,在
,在 内单调递增,
内单调递增,
可得 

练习册系列答案
相关题目
 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, 分,且满足
分,且满足 .
. ,求△
,求△ 是第四象限角,则
是第四象限角,则 _______________
_______________ 上的函数
上的函数 且
且 时,
时, 则
则 ( )
( ) C.1 D.-
C.1 D.- 的单调函数
的单调函数
 ,都有
,都有 ,
, 是方程
是方程 的一个解,且
的一个解,且 ,则
,则 _ _
_ _ 中,
中, ,
, ,点
,点 是斜边
是斜边 上的一个三等分点,则
上的一个三等分点,则 ( )
( ) C.
C. D.4
D.4 ,则
,则 .
. 的图象的大致形状是( )
的图象的大致形状是( ) 
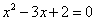 则x=1”的逆否命题为“若
则x=1”的逆否命题为“若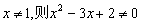 ”
”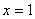 ”是“
”是“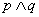 为假命题,则p、q均为假命题
为假命题,则p、q均为假命题