题目内容
20. 在直三棱柱ABC-A1B1C1中,已知∠BCA=90°,∠BAC=60°,AC=4,E为AA1的中点,点F为BE的中点,点H在线段CA1上,且A1H=3HC,则线段FH的长为( )
在直三棱柱ABC-A1B1C1中,已知∠BCA=90°,∠BAC=60°,AC=4,E为AA1的中点,点F为BE的中点,点H在线段CA1上,且A1H=3HC,则线段FH的长为( )| A. | $2\sqrt{3}$ | B. | 4 | C. | $\sqrt{13}$ | D. | 3 |
分析 以C为原点建立空间直角坐标系,则C(0,0,0),A(0,4,0),B(0,4$\sqrt{3}$,0),E(4,0,m),A1(4,0,2m).可得F(2,2$\sqrt{3}$,$\frac{m}{2}$),H(1,0,$\frac{m}{2}$),利用空间两点间的距离公式计算即可.
解答 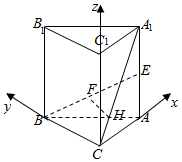 解:如图,以C为原点建立空间直角坐标系,
解:如图,以C为原点建立空间直角坐标系,
∵∠BCA=90°,∠BAC=60°,AC=4,∴BC=4$\sqrt{3}$,
则C(0,0,0),A(0,4,0),B(0,4$\sqrt{3}$,0),E(4,0,m),A1(4,0,2m).
∵点F为BE的中点,∴F(2,2$\sqrt{3}$,$\frac{m}{2}$),
∵点H在线段CA1上,且A1H=3HC,∴H(1,0,$\frac{m}{2}$)
∴FH=$\sqrt{(2-1)^{2}+(2\sqrt{3}-0)^{2}+(\frac{m}{2}-\frac{m}{2})^{2}}$=$\sqrt{13}$.
故选C.
点评 本题考查了空间两点间的距离公式计算,属于基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
14.某市为加强市民的环保意识,组织了“支持环保”签名活动.分别在甲、乙、丙、丁四个不同的场地是进行支持签名获得,统计数据表格如下:
(1)若采用分层抽样的方式从获得签名的人中抽取10名幸运之星,再从10名幸运之星中任选2人接受电视台采访,求这2人来自不同场地的概率;
(2)电视台记者对场地的签名人进行了是否“支持环保”的问卷调查,统计结果如下(单位:人);现定义W=|$\frac{a}{a+b}-\frac{c}{c+d}$|,请根据W的值判断,能否在犯错的概率不超过0.01的前提下认为“支持环保”与性别有关.
临界值表:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.其中n=a+b+c+d.
| 公园 | 甲 | 乙 | 丙 | 丁 |
| 获得签名人数 | 45 | 60 | 30 | 15 |
(2)电视台记者对场地的签名人进行了是否“支持环保”的问卷调查,统计结果如下(单位:人);现定义W=|$\frac{a}{a+b}-\frac{c}{c+d}$|,请根据W的值判断,能否在犯错的概率不超过0.01的前提下认为“支持环保”与性别有关.
| 有兴趣 | 无兴趣 | 合计 | |
| 男 | 25 | 5 | 30 |
| 女 | 15 | 15 | 30 |
| 合计 | 40 | 20 | 60 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
12.袋中装有编号分别为1,2,3,…,2n的2n(n∈N*)个小球,现将袋中的小球分给A,B,C三个盒子,每次从袋中任意取出两个小球,将其中一个放入A盒子,如果这个小球的编号是奇数,就将另一个放入B盒子,否则就放入C盒子,重复上述操作,直到所有小球都被放入盒中,则下列说法一定正确的是( )
| A. | B盒中编号为奇数的小球与C盒中编号为偶数的小球一样多 | |
| B. | B盒中编号为偶数的小球不多于C盒中编号为偶数的小球 | |
| C. | B盒中编号为偶数的小球与C盒中编号为奇数的小球一样多 | |
| D. | B盒中编号为奇数的小球多于C盒中编号为奇数的小球 |
9.已知a,5,b组成公差为d的等差数列,又a,4,b组成等比数列,则公差d=( )
| A. | -3 | B. | 3 | C. | -3或3 | D. | 2或$\frac{1}{2}$ |