题目内容
【题目】已知函数/ ![]() (
(![]() 为常数)的图像与
为常数)的图像与![]() 轴交于点
轴交于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
(1)求![]() 的值及函数的极值;
的值及函数的极值;
(2)证明:当![]() 时,
时, ![]() ;
;
(3)证明:对任意给定的正数![]() ,总存在
,总存在![]() ,使得当
,使得当![]() ,恒有
,恒有![]() .
.
【答案】(1) ![]() ;(2)证明见解析;(3) 证明见解析.
;(2)证明见解析;(3) 证明见解析.
【解析】试题分析: (1) 求出![]() ,由
,由 ![]() 可得
可得![]() 的值,
的值, ![]() 得增区间,
得增区间, ![]() 得减区间,从而可得函数的极值;(2) 令
得减区间,从而可得函数的极值;(2) 令![]() ,研究函数的单调性,只需证明
,研究函数的单调性,只需证明![]() 的最小值大于零即可;(3) 对任意给定的正数c,取
的最小值大于零即可;(3) 对任意给定的正数c,取![]()
由(2)知,当x>0时, ![]() ,所以
,所以![]() .当
.当![]() 时,
时, ![]() ,从而可得结论.
,从而可得结论.
试题解析:(1)由![]() ,得
,得![]() .
.
又![]() ,得
,得![]() .
.
所以![]() .令
.令![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增.
单调递增.
所以当![]() 时,
时, ![]() 取得极小值
取得极小值![]() 无极大值.
无极大值.
(2)令![]() ,则
,则![]() .
.
由(1)得![]() ,故
,故![]() 在R上单调递增,
在R上单调递增,
又![]() ,因此,当
,因此,当![]() 时,
时, ![]() ,即
,即![]() .
.
(3)解法一:①若![]() ,则
,则![]() .又由(2)知,当
.又由(2)知,当![]() 时,
时, ![]() .
.
所以当![]() 时,
时, ![]() .取
.取![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
②若![]() ,令
,令![]() ,要使不等式
,要使不等式![]() 成立,只要
成立,只要![]() 成立.
成立.
而要使![]() 成立,则只要
成立,则只要![]() ,只要
,只要![]() 成立.
成立.
令![]() ,则
,则![]() .
.
所以当![]() 时,
时, ![]() 在
在![]() 内单调递增.
内单调递增.
取![]() ,所以
,所以![]() 在
在![]() 内单调递增.
内单调递增.
又![]() =
=![]() .
.
易![]() .所以
.所以![]() .
.
即存在![]() ,当
,当![]() 时,恒
时,恒![]() .
.
综上,对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
解法二:对任意给定的正数c,取![]()
由(2)知,当x>0时, ![]() ,所以
,所以![]()
当![]() 时,
时, ![]()
因此,对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]()

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002, ,800进行编号;
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;
(下面摘取了第7行到第9行)

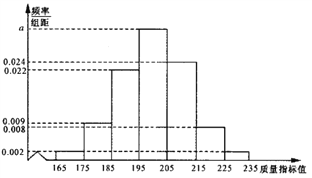
(2)抽取的100的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42,若在该样本中,数学成绩优秀率是30%,求a,b的值:
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
(3)在地理成绩及格的学生中,已知![]() 求数学成绩为优秀的人数比及格的人数少的概率.
求数学成绩为优秀的人数比及格的人数少的概率.