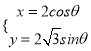题目内容
【题目】已知![]() 是椭圆C:
是椭圆C: ![]() 上一点,点P到椭圆C的两个焦点的距离之和为
上一点,点P到椭圆C的两个焦点的距离之和为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设A,B是椭圆C上异于点P的两点,直线PA与直线![]() 交于点M,
交于点M,
是否存在点A,使得![]() ?若存在,求出点A的坐标;若不存在,请说明理由.
?若存在,求出点A的坐标;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)存在点A(
;(Ⅱ)存在点A(![]() ,
, ![]() ),使得
),使得![]() .
.
【解析】试题分析:(Ⅰ)椭圆过点P(0,1)可得b=1,由点P到两焦点距离和为![]() ,可得
,可得![]() ,进而可得结果;(Ⅱ)设
,进而可得结果;(Ⅱ)设![]() ,依题意得:直线
,依题意得:直线![]() 的斜率存在,
的斜率存在,
则直线![]() 的方程为:
的方程为: ![]() ,又
,又![]() 等价于
等价于![]() 且点A在y轴的右侧,
且点A在y轴的右侧,
从而![]() , 从而可得结果.
, 从而可得结果.
.
试题解析:
(Ⅰ)由椭圆C: ![]() 过点P(0,1)可得b=1,
过点P(0,1)可得b=1,
又点P到两焦点距离和为![]() ,可得
,可得![]() ,
,
所以椭圆C的方程![]() .
.
(Ⅱ)设A(m,n),依题意得:直线PA的斜率存在,
则直线PA的方程为: ![]() ,
,
令x=4, ![]() ,即M
,即M![]() ,
,
又![]() 等价于
等价于![]() 且点A在y轴的右侧,
且点A在y轴的右侧,
从而![]() ,
,
因为点A在y轴的右侧,
所以![]() , 解得
, 解得 ![]() ,
,
由点A在椭圆上,解得: ![]() ,
,
于是存在点A(![]() ,
, ![]() ),使得
),使得![]() .
.
【方法点晴】本题主要考查待定系数法求椭圆的标准方程以及解析几何中的存在性问题,属于难题.解决存在性问题,先假设存在,推证满足条件的结论,若结论正确则存在,若结论不正确则不存在,注意:①当条件和结论不唯一时要分类讨论;②当给出结论而要推导出存在的条件时,先假设成立,再推出条件;③当条件和结论都不知,按常规方法题很难时采取另外的途径.

 阅读快车系列答案
阅读快车系列答案【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1) 根据题意完成表格;
(2) 是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
参考公式及数据: 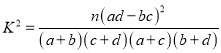 ,其中
,其中![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |