题目内容
以坐标原点为极点,横轴的正半轴为极轴的极坐标系下,有曲线C: ,过极点的直线
,过极点的直线 (
(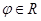 且
且 是参数)交曲线C于两点0,A,令OA的中点为M.
是参数)交曲线C于两点0,A,令OA的中点为M.
(1)求点M在此极坐标下的轨迹方程(极坐标形式).
(2)当 时,求M点的直角坐标.
时,求M点的直角坐标.
(1) ,(2)
,(2)
解析试题分析:(1)因为OA的中点为M.,而OA= ,所以OM=
,所以OM= OA,点M在此极坐标下的轨迹方程是
OA,点M在此极坐标下的轨迹方程是 。
。
(2) 时,
时, ,所以x=cos
,所以x=cos =
= ,y=sin
,y=sin =
= ,即M点的直角坐标是
,即M点的直角坐标是 。
。
考点:本题主要考查简单曲线的极坐标方程,直角坐标与极坐标的互化。
点评:简单题,因为OA的中点为M.,所以OM= OA,利用的是几何关系法。
OA,利用的是几何关系法。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知A(2,1),B(3,2),C(-1,4),则△ABC是( )
| A.直角三角形 |
| B.锐角三角形 |
| C.钝角三角形 |
| D.等腰直角三角形 |
 过点P(-2,-4)的直线
过点P(-2,-4)的直线 为参数)与曲线C相交于点M,N两点.
为参数)与曲线C相交于点M,N两点. 的普通方程;
的普通方程; ,试求:
,试求: 得到曲线
得到曲线 ,则曲线
,则曲线 =1,以极点为原点,极轴为
=1,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 为参数)。
为参数)。 得到曲线
得到曲线 ,设曲线
,设曲线 ,求
,求 的最小值。
的最小值。
 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值. 轴非负半轴重合.直线
轴非负半轴重合.直线 的参数方程为:
的参数方程为: (
( 为参数),曲线
为参数),曲线 的极坐标方程为:
的极坐标方程为: .
. 两点,求
两点,求 的值.2
的值.2 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点 
 ,且
,且 .
. 与
与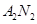 交点的轨迹
交点的轨迹 的方程;
的方程; (
( )是轨迹
)是轨迹 是轨迹
是轨迹 的斜率
的斜率 与直线
与直线 的斜率
的斜率 满足
满足 ,试探究直线
,试探究直线 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由. 中,以
中,以 极点,
极点, 轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为 分别为
分别为 与
与 轴的交点
轴的交点 的极坐标
的极坐标 的中点为
的中点为 ,求直线
,求直线 的极坐标方程
的极坐标方程