题目内容
已知平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,
(1)求AC′的长;(如图所示)
(2)求
与
的夹角的余弦值.
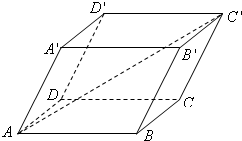
(1)求AC′的长;(如图所示)
(2)求
| AC/ |
| AC |

(1)可得
=
+
=
+
+
,
故|
|2=|
+
+
|2=
2+
2+
2
+2(
•
+
•
+
•
)
=42+32+52+2(4×3×0+4×5×
+3×5×
)=85
故AC′的长等于|
|=
(2)由(1)可知
=
+
+
,|
|=
故
′•
=(
+
+
)•(
+
)
=
2+2
•
+
2+
•
+
•
=42+2×4×3×0+32+5×4×
+5×3×
=
又|
|=
=
=
=5
故
| AC′ |
| AC |
| CC′ |
| AB |
| AD |
| AA′ |
故|
| AC′ |
| AB |
| AD |
| AA′ |
| AB |
| AD |
| AA′ |
+2(
| AB |
| AD |
| AB |
| AA′ |
| AD |
| AA′ |
=42+32+52+2(4×3×0+4×5×
| 1 |
| 2 |
| 1 |
| 2 |
故AC′的长等于|
| AC′ |
| 85 |
(2)由(1)可知
| AC′ |
| AB |
| AD |
| AA′ |
| AC′ |
| 85 |
故
| AC |
| AC |
| AB |
| AD |
| AA′ |
| AB |
| AD |
=
| AB |
| AB |
| AD |
| AD |
| AA′ |
| AB |
| AA′ |
| AD |
=42+2×4×3×0+32+5×4×
| 1 |
| 2 |
| 1 |
| 2 |
| 85 |
| 2 |
又|
| AC |
(
|
|
| 42+0+32 |
故
<

练习册系列答案
 天天向上一本好卷系列答案 天天向上一本好卷系列答案 小学生10分钟应用题系列答案 小学生10分钟应用题系列答案
相关题目
|
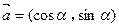 ,
,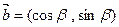
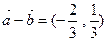 ,
,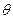 为
为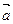 与
与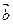 的夹角,求
的夹角,求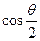 。
。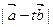 的值最小?
的值最小? 与
与 ,其中
,其中
 ,求
,求 和
和 的值;
的值; ,求
,求 的值域。
的值域。